已知数列{an}的前n项和为Sn＝3n－1.
(1)求数列{an}的通项公式；
(2)若bn＝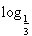
(Sn＋1)，求数列{bnan}的前n项和Tn.
（1）an＝2×3n－1（2）－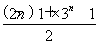
，n∈N*
【解析】(1)当n＝1时，a1＝S1＝2，
当n≥2时，an＝Sn－Sn－1＝(3n－1)－(3n－1－1)＝2×3n－1，综上所述，an＝2×3n－1.
(2)bn＝
(Sn＋1)＝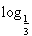
3n＝－n，所以bnan＝－2n×3n－1，
Tn＝－2×1－4×31－6×32－…－2n×3n－1，
3Tn＝－2×31－4×32－…－2(n－1)×3n－1－2n×3n，相减，得
－2Tn＝－2×1－2×31－2×32－…－2×3n－1＋2n×3n
＝－2×(1＋31＋32＋…＋3n－1)＋2n×3n，
所以Tn＝(1＋31＋32＋…＋3n－1)－n×3n＝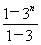
－n×3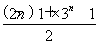n＝－，n∈N*
文敬图书课时先锋系列答案科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第2课时练习卷（解析版） 题型：填空题
α、β、γ是三个平面，a、b是两条直线，有下列三个条件：①a∥γ，b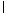
β；②a∥γ，b∥β；③b∥β，a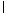γ.如果命题“α∩β＝a，b
γ，且________，则a∥b”为真命题，则可以在横线处填入的条件是________(填序号)．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷（解析版） 题型：解答题
设{an}是首项为a，公差为d的等差数列(d≠0)，Sn是其前n项和．记bn＝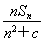
，n∈N*，其中c为实数．
(1)若c＝0，且b1，b2，b4成等比数列，证明：Snk＝n2Sk(k，n∈N*)；
(2)若{bn}是等差数列，证明：c＝0.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第5课时练习卷（解析版） 题型：解答题
已知数列{an}是首项为1，公差为d的等差数列，数列{bn}是首项为1，公比为q(q＞1)的等比数列．
(1)若a5＝b5，q＝3，求数列{an·bn}的前n项和；
(2)若存在正整数k(k≥2)，使得ak＝bk.试比较an与bn的大小，并说明理由．．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第4课时练习卷（解析版） 题型：解答题
已知等差数列{an}是递增数列，且满足a4·a7＝15，a3＋a8＝8.
(1)求数列{an}的通项公式；
(2)令bn＝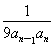
(n≥2)，b1＝
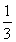，求数列{bn}的前n项和Sn.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第4课时练习卷（解析版） 题型：填空题
在数列{an}中，若a1＝1，an＋1＝an＋2(n≥1)，则该数列的通项an＝________．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第3课时练习卷（解析版） 题型：填空题
已知两个数k＋9和6－k的等比中项是2k，则k＝________．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第二章第9课时练习卷（解析版） 题型：填空题
已知函数f(x)＝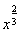
，x∈[－1，8]，函数g(x)＝ax＋2，x∈[－1，8]，若存在x∈[－1，8]，使f(x)＝g(x)成立，则实数a的取值范围是________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
