
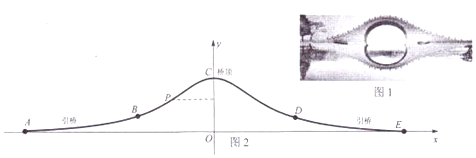
分析 (1)设出方程,利用B为衔接点,即可求出曲线段AB在图纸上对应函数的解析式,并写出定义域;
(2)分类讨论,求最值,即可得出结论.
解答 解:(1)由题意A为抛物线的顶点,设A(a,0)(a<-2),则可设方程为y=λ(x-a)2(a≤x≤-2,λ>0),y′=2λ(x-a).
曲线段BCD在图纸上的图形对应函数的解析式为y=$\frac{8}{4+{x}^{2}}$(x∈[-2,2]),
y′=$\frac{-16x}{(4+{x}^{2})^{2}}$,且B(-2,1),则曲线在B处的切线斜率为$\frac{1}{2}$,
∴$\left\{\begin{array}{l}{λ(-2-a)^{2}=1}\\{2λ(-2-a)=\frac{1}{2}}\end{array}\right.$,∴a=-6,λ=$\frac{1}{16}$,
∴曲线段AB在图纸上对应函数的解析式为y=$\frac{1}{16}(x+6)^{2}$(-6≤x≤-2);
(2)设P为曲线段AC上任意一点.
①P在曲线段AB上,则通过该点所需要的爬坡能力(MP)1=$(-x)•\frac{1}{8}(x+6)$=$-\frac{1}{8}[(x+3)^{2}-9]$,
在[-6,-3]上为增函数,[-3,-2]上是减函数,最大为$\frac{9}{8}$米;
②P在曲线段BC上,则通过该点所需要的爬坡能力(MP)2=$(-x)•\frac{-16x}{(4+{x}^{2})^{2}}$=$\frac{16{x}^{2}}{(4+{x}^{2})^{2}}$(x∈[-2,0]),
设t=x2,t∈[0,4],(MP)2=y=$\frac{16t}{(4+t)^{2}}$.
t=0,y=0;0<t≤4,y=$\frac{16}{\frac{16}{t}+t+8}$≤1(t=4取等号),此时最大为1米.
由上可得,最大爬坡能力为$\frac{9}{8}$米;
∵0.8<$\frac{9}{8}$<1.5<2,
∴游客踏乘不能顺利通过该桥;蓄电池动力和内燃机动力能顺利通过该桥.
点评 本题考查利用数学知识解决实际问题,考查导数知识的运用,确定函数的解析式是关键.


科目:高中数学 来源: 题型:选择题
| A. | 若$λ\overrightarrow{a}+μ\overrightarrow{b}$=$\overrightarrow{0}$,则λ=μ=0 | B. | 若$\overrightarrow{a}•\overrightarrow{b}$=0,则$\overrightarrow{a}$∥$\overrightarrow{b}$ | ||
| C. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为|$\overrightarrow{a}$| | D. | 若$\overrightarrow{a}⊥\overrightarrow{b}$,则$\overrightarrow{a}$•$\overrightarrow{b}$=($\overrightarrow{a}$$•\overrightarrow{b}$)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {1,2,0,-1} | C. | (-1,2] | D. | {1.5,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2
如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com