分析:(1)先令x=y=0,解得f(0),再令x=0得f(0)-f(y)=f(-y)即f(y)+f(-y)=0由奇偶性定义判断.
(2)由
x1=,xn+1=(n∈N*)易知0<x
n<1,由主条件得
f(xn)-f(-xn)=f()和f(x)在(-1,1)上为奇函数得f(x
n+1)=2f(x
n)再由f(x
1)=1,得到f(x
n)是以1为首项,2为公比的等比数列求解.
(3)由(2)将
+++<成立转化为
2-<恒成立,由
2-<2得
≥2求解.
解答:解:(1)当x=y=0时,f(0)=0,再令x=0得f(0)-f(y)=f(-y)即f(y)+f(-y)=0
∴f(x)在(-1,1)上为为奇函数.
(2)由
x1=,xn+1=(n∈N*)易知:{x
n}中0<x
n<1,
∵
f(xn)-f(-xn)=f()且f(x)在(-1,1)上为奇函数
∴f(x
n+1)=2f(x
n)由
f()=1,
x1=∴f(x
1)=1
∴f(x
n)是以1为首项,2为公比的等比数列∴f(x
n)=2
n-1(3)
+++=1++++=2-假设存在m使得
+++<成立,即
2-<恒成立,
∵
2-<2,
∴
≥2,
∴m≥16,
∴存在自然数m≥16,
使得
+++<成立,此时最小的自然数m=16.
点评:本题主要考查抽象抽象函数判断奇偶性及求解析式,进而转化为数列模型研究等比数列求和解决恒成立问题.



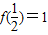 ,且满足x,y∈(-1,1)有
,且满足x,y∈(-1,1)有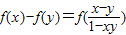 .对数列{xn}有
.对数列{xn}有
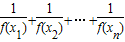 <
<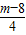 成立?若存在,求出m的最小值.
成立?若存在,求出m的最小值. ,且满足x,y∈(-1,1)有
,且满足x,y∈(-1,1)有 .对数列{xn}有
.对数列{xn}有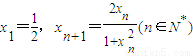
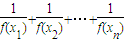 <
< 成立?若存在,求出m的最小值.
成立?若存在,求出m的最小值.