[题目]如图.半径为1.圆心角为的圆弧上有一点C． (1)若C为圆弧AB的中点.点D在线段OA上运动.求| |的最小值,(2)若D.E分别为线段OA.OB的中点.当C在圆弧上运动时.求的取值范围．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图，半径为1，圆心角为的圆弧上有一点C．
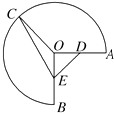
（1）若C为圆弧AB的中点，点D在线段OA上运动，求| |的最小值；
（2）若D，E分别为线段OA，OB的中点，当C在圆弧上运动时，求的取值范围．

【答案】
（1）解：以O为原点，OA为x轴建立直角坐标系，

则

设D（t，0）（0≤t≤1），则，

所以，

当时，

（2）解：由题意，设C（cosθ，sinθ），

所以 = ．

因为，则，所以

【解析】（1）以O为原点，以OA为x轴正方向，建立图示坐标系，设D（t，0）（0≤t≤1），求出C坐标，推出，然后求出模的最小值．（2）设C（cosθ，sinθ），，求出的表达式，即可求出的取值范围．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】．
（1）若时，，求cos4x的值；
（2）将的图象向左移，再将各点横坐标伸长为原来的2倍，纵坐标不变，得y=g（x），若关于g（x）+m=0在区间上的有且只有一个实数解，求m的范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图是市儿童乐园里一块平行四边形草地ABCD，乐园管理处准备过线段AB上一点E设计一条直线EF（点F在边BC或CD上，不计路的宽度），将该草地分为面积之比为2：1的左、右两部分，分别种植不同的花卉．经测量得AB=18m，BC=10m，∠ABC=120°．设EB=x，EF=y（单位：m）．
（1）当点F与C重合时，试确定点E的位置；
（2）求y关于x的函数关系式；
（3）请确定点E、F的位置，使直路EF长度最短．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知x∈（1，5），则函数y= + 的最小值为．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】公元263年左右，我国数学有刘徽发现当圆内接多边形的边数无限增加时，多边形的面积可无限逼近圆的面积，并创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14，这就是著名的“徽率”．某同学利用刘徽的“割圆术”思想设计了一个计算圆周率的近似值的程序框图如图，则输出S的值为（参考数据：sin15°=0.2588，sin7.5°=0.1305）（）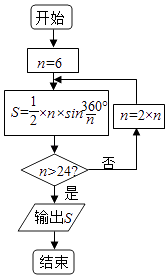

A.2.598
B.3.106
C.3.132
D.3.142

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知首项为1的正项数列{an}满足an+12+an2＜，n∈N* ， Sn为数列{an}的前n项和．
（1）若a2= ，a3=x，a4=4，求x的取值范围；
（2）设数列{an}是公比为q的等比数列，若＜Sn+1＜2Sn ， n∈N* ，求q的取值范围；
（3）若a1 ， a2 ， …，ak（k≥3）成等差数列，且a1+a2+…+ak=120，求正整数k的最小值，以及k取最小值时相应数列a1 ， a2 ， …，ak ．