
【题目】设f(x)为奇函数,且f(x)在(﹣∞,0)内是增函数,f(﹣2)=0,则xf(x)>0的解集为 .
【答案】(﹣∞,﹣2)∪(2,+∞)
【解析】解:不等式xf(x)>0等价为 ![]() 或
或 ![]() ,
,
∵f(x)为奇函数且在(﹣∞,0)内是增函数,f(﹣2)=0,
∴f(x)为奇函数且在(0,+∞)内是增函数,f(2)=0,
但当x>0时,不等式f(x)>0等价为f(x)>f(2),即x>2,
当x<0时,不等式f(x)<0等价为f(x)<f(﹣2),即x<﹣2,
综上x>2或x<﹣2,
故不等式xf(x)>0的解集是(﹣∞,﹣2)∪(2,+∞),
所以答案是:(﹣∞,﹣2)∪(2,+∞).
【考点精析】本题主要考查了奇偶性与单调性的综合的相关知识点,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月产量如表(单位:辆):
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆。
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本。将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)已知幂函数f(x)=(﹣2m2+m+2)x﹣2m+1为偶函数,求函数f(x)的解析式;
(2)已知x+x﹣1=3(x>1),求x2﹣x﹣2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2﹣ax+3,且对任意的实数x都有f(4﹣x)=f(x)成立.
(1)求实数a的值;
(2)求函数f(x)在区间[0,3]上的值域;
(3)要得到函数y=x2的图象只需要将二次函数y=f(x)的图象做怎样的变换得到.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第31届夏季奥林匹克运动会于2016年8月5日至8月21日在巴西里约热内卢举行.如表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
第30届伦敦 | 第29届北京 | 第28届雅典 | 第27届悉尼 | 第26届亚特兰大 | |
中国 | 38 | 51 | 32 | 28 | 16 |
俄罗斯 | 24 | 23 | 27 | 32 | 26 |
(1)根据表格中两组数据在答题卡上完成近五届奥运会两国代表团获得的金牌数的茎叶图,并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度(不要求计算出具体数值,给出结论即可);
(2)如表是近五届奥运会中国代表团获得的金牌数之和![]() (从第26届算起,不包括之前已获得的金牌数)随时间
(从第26届算起,不包括之前已获得的金牌数)随时间![]() 变化的数据:
变化的数据:
时间 | 26 | 27 | 28 | 29 | 30 |
金牌数之和 | 16 | 44 | 76 | 127 | 165 |
作出散点图如图:

由图可以看出,金牌数之和![]() 与时间
与时间![]() 之间存在线性相关关系,请求出
之间存在线性相关关系,请求出![]() 关于
关于![]() 的线性回归方程,并预测到第32届奥运会时中国代表团获得的金牌数之和为多少?
的线性回归方程,并预测到第32届奥运会时中国代表团获得的金牌数之和为多少?
附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣x+2a﹣1(a>0).
(1)若f(x)在区间[1,2]为单调增函数,求a的取值范围;
(2)设函数f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式;
(3)设函数 ![]() ,若对任意x1 , x2∈[1,2],不等式f(x1)≥h(x2)恒成立,求实数a的取值范围.
,若对任意x1 , x2∈[1,2],不等式f(x1)≥h(x2)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,顶点为
,顶点为![]() ,且
,且![]() .
.
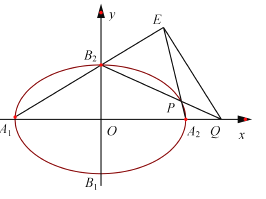
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆
是椭圆![]() 上除顶点外的任意点,直线
上除顶点外的任意点,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .设
.设![]() 的斜率为
的斜率为![]() ,
, ![]() 的斜率为
的斜率为![]() ,试问
,试问![]() 是否为定值?并说明理由.
是否为定值?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com