
【题目】如图,已知四棱锥![]() 的底面为矩形,D为
的底面为矩形,D为![]() 的中点,AC⊥平面BCC1B1.
的中点,AC⊥平面BCC1B1.
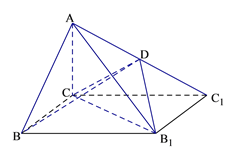
(Ⅰ)证明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=![]() ,
,
(1)求BD的长;
(2)求B1D与平面ABB1所成角的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ) (1)![]() ,(2)
,(2)![]() .
.
【解析】试题分析:(Ⅰ)利用中位线定理得出DE//AB,即可证得;
(Ⅱ)(1)在![]() 中,利用勾股定理运算即可;
中,利用勾股定理运算即可;
(2)以C为原点,CB所在的直线为x轴、CC1为y轴建立空间直角坐标系,利用向量求解线面角即可.
试题解析:
(Ⅰ)证明:连结![]() 交
交![]() 于E,连结DE,
于E,连结DE,
∵D、E分别为![]() 和
和![]() 的中点,
的中点,
∴DE//AB,
又∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴AB//平面CDB1;
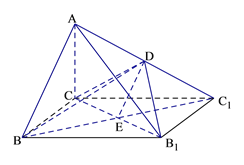
(Ⅱ)(1)∵AC⊥平面BCC1B1, ![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
在![]() ,∵BC=1,
,∵BC=1, ![]() ,
,
∴![]() ;
;
【注:以上加灰色底纹的条件不写不扣分!】
(2)依题意知AC、BC、CC1两两互相垂直,以C为原点,CB所在的直线为x轴、CC1为y轴建立空间直角坐标系如图示,
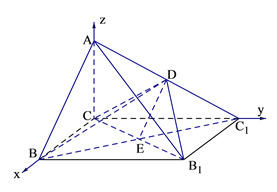
易得![]() ,
, ![]() ,
,
![]() ,
, 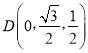 ,
,
故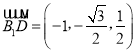 ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由![]() 得
得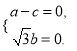 令
令![]() 得
得![]() ,
,
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则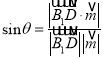
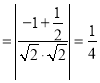 ,
,
即![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.
【其它解法请参照给分,如先用体积法求出点D到平面ABB1的距离![]() ,(10分)再用公式
,(10分)再用公式![]() 算
算![]() 与平面
与平面![]() 所成角的正弦值(12分)】
所成角的正弦值(12分)】


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】(本题满分12分)某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,用最小二乘法求出y与x的回归方程![]() ;
;
(3)预测销售额为115万元时,大约需要多少万元广告费。
参考公式:回归方程为![]() 其中
其中 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-![]() (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.

(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,求函数
时,求函数![]() 的最小值
的最小值![]() ;
;
(3)是否存在非负实数![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() ,与
,与![]() ,
,![]() 各有一个交点,当
各有一个交点,当![]() 时,这两个交点间的距离为2,当
时,这两个交点间的距离为2,当![]() ,这两个交点重合.
,这两个交点重合.
(1)分别说明![]() ,
,![]() 是什么曲线,并求出
是什么曲线,并求出![]() 与
与![]() 的值;
的值;
(2)设当![]() 时,
时,![]() 与
与![]() ,
,![]() 的交点分别为
的交点分别为![]() ,当
,当![]() ,
,![]() 与
与![]() ,
,![]() 的交点分别为
的交点分别为![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据四川省民政厅报告,2013年6月29日以来,四川省中东部出现强降雨天气过程,局地出现大暴雨.暴雨洪涝灾害已造成遂宁、德阳、绵阳等12市34县(市、区)244万人受灾,共造成直接经济损失85502.41万元.适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).
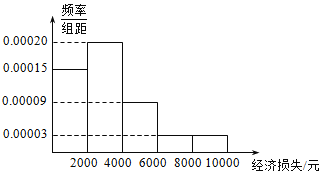
(1)若先从损失超过6000元的居民中随机抽出2户进行调查,求这2户不在同一小组的概率;(2)洪灾过后小区居委会号召小区居民为洪灾重灾区捐款,小王调查的50户居民的捐款情况如表,在表格空白处填写正确的数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?

P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:临界值表参考公式:K2=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com