
【题目】已知![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 为坐标原点,是否存在常数
为坐标原点,是否存在常数![]() ,使得
,使得![]() 恒成立?请说明理由.
恒成立?请说明理由.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】为了引导居民合理用电,国家决定实行合理的阶梯电价,居民用电原则上以住宅为单位(一套住宅为一户).

某市随机抽取10户同一个月的用电情况,得到统计表如下:

(1)若规定第一阶梯电价每度0.5元,第二阶梯超出第一阶梯的部分每度0.6元,第三阶梯超出第二阶梯每度0.8元,试计算![]() 居民用电户用电410度时应交电费多少元?
居民用电户用电410度时应交电费多少元?
(2)现要在这10户家庭中任意选取3户,求取到第二阶梯电量的户数的分布列与期望;
(3)以表中抽到的10户作为样本估计全市居民用电,现从全市中依次抽取10户,若抽到![]() 户用电量为第一阶梯的可能性最大,求
户用电量为第一阶梯的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年五月最受七中学子期待的学生活动莫过于学生节,在每届学生节活动中,着七中校服的布偶“七中熊”尤其受同学和老师欢迎.已知学生会将在学生节当天售卖“七中熊”,并且会将所获得利润全部捐献于公益组织.为了让更多同学知晓,学生会宣传部需要前期在学校张贴海报宣传,成本为250元,并且当学生会向厂家订制![]() 只“七中熊”时,需另投入成本
只“七中熊”时,需另投入成本![]() ,
,![]() (元),
(元),![]() .通过市场分析, 学生会订制的“七中熊”能全部售完.若学生节当天,每只“七中熊”售价为70元,则当销量为______只时,学生会向公益组织所捐献的金额会最大.
.通过市场分析, 学生会订制的“七中熊”能全部售完.若学生节当天,每只“七中熊”售价为70元,则当销量为______只时,学生会向公益组织所捐献的金额会最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正项数列:![]() ,满足:
,满足:![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为2的等比数列.
是公比为2的等比数列.
(1)若![]() ,求数列
,求数列![]() 的所有项的和
的所有项的和![]() ;
;
(2)若![]() ,求
,求![]() 的最大值;
的最大值;
(3)是否存在正整数![]() ,满足
,满足![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 分别为棱
分别为棱![]() 上的动点(
上的动点(![]() 与所在棱的端点不重合),且满足
与所在棱的端点不重合),且满足![]() .
.
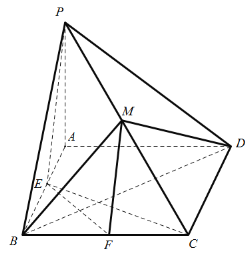
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,若an2﹣an﹣12=p,(n≥2,n∈N*,p为常数),则称{an}为“等方差数列”,下列是对“等方差数列“的判断:
①若{an}是等方差数列,则{an2}是等差数列;
②{(﹣1)n}是等方差数列;
③若{an}是等方差数列,则{akn}(k∈N*,k为常数)也是等方差数列;
④若{an}既是等方差数列,又是等差数列,则该数列为常数列.
其中正确命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知递增数列{an}前n项和为Sn,且满足a1=3,4Sn﹣4n+1=an2,设bn![]() (n∈N*)且数列{bn}的前n项和为Tn
(n∈N*)且数列{bn}的前n项和为Tn
(Ⅰ)求证:数列{an}为等差数列;
(Ⅱ)若对任意的n∈N*,不等式λTn![]() n
n![]() (﹣1)n+1恒成立,求实数λ的取值范围.
(﹣1)n+1恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列各命题:
①两两相交且不共点的三条直线确定一个平面:
②若真线![]() 不平行于平面
不平行于平面![]() ,则直线
,则直线![]() 与平面
与平面![]() 有公共点:
有公共点:
③若两个平面垂直,则一个平面内的已知直线必垂直于另一个平面的无数条直线:
④若两个二面角的两个面分别对应垂直,则这两个二面角相等或互补.
则其中正确的命题共有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com