
【题目】2018年反映社会现实的电影《我不是药神》引起了很大的轰动,治疗特种病的创新药研发成了当务之急.为此,某药企加大了研发投入,市场上治疗一类慢性病的特效药品![]() 的研发费用
的研发费用![]() (百万元)和销量
(百万元)和销量![]() (万盒)的统计数据如下:
(万盒)的统计数据如下:
研发费用 | 2 | 3 | 6 | 10 | 13 | 15 | 18 | 21 |
销量 | 1 | 1 | 2 | 2.5 | 3.5 | 3.5 | 4.5 | 6 |
(1)根据数据用最小二乘法求出![]() 与
与![]() 的线性回归方程
的线性回归方程![]() (系数用分数表示,不能用小数);
(系数用分数表示,不能用小数);
(2)该药企准备生产药品![]() 的三类不同的剂型
的三类不同的剂型![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() ,第二次检测时,三类剂型
,第二次检测时,三类剂型![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() .两次检测过程相互独立,设经过两次检测后
.两次检测过程相互独立,设经过两次检测后![]() ,
,![]() ,
,![]() 三类剂型合格的种类数为
三类剂型合格的种类数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:(1)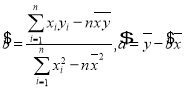 (2)
(2)![]() .
.
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,O、E分别是BD、BC的中点,![]() ,
,![]() .
.
(1)求证:![]() 平面BCD;
平面BCD;
(2)求异面直线AB与CD所成角的余弦值;
(3)求点E到平面ACD的距离。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的方程为![]() .在以原点O为极点,x轴正半轴为极轴的极坐标系中,P的极坐标为
.在以原点O为极点,x轴正半轴为极轴的极坐标系中,P的极坐标为![]() ,直线l过点P.
,直线l过点P.
(1)若直线l与OP垂直,求直线l的直角标方程:
(2)若直线l与曲线C交于A,B两点,且![]() ,求直线l的倾斜角.
,求直线l的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
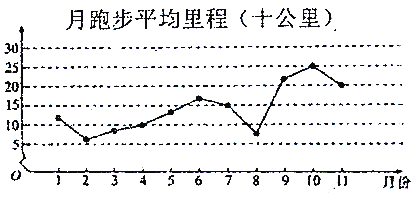
【题目】微信运动,是由腾讯开发的一个类似计步数据库的公众账号.用户可以通过关注微信运动公众号查看自己每天或每月行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
根据折线图,下列结论正确的是( )
A. 月跑步平均里程的中位数为![]() 月份对应的里程数
月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在![]() 、
、![]() 月
月
D. ![]() 月至
月至![]() 月的月跑步平均里程相对于
月的月跑步平均里程相对于![]() 月至
月至![]() 月,波动性更小,变化比较平稳
月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() 成等差数列;②
成等差数列;②![]() 成等比数列;③
成等比数列;③![]() 三个条件中任选一个,补充在下面的问题中,并加以解答.
三个条件中任选一个,补充在下面的问题中,并加以解答.
已知![]() 的内角
的内角![]() 所对的边分别是
所对的边分别是![]() ,面积为
,面积为![]() .若__________,且
.若__________,且![]() ,试判断
,试判断![]() 的形状.
的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点
的左、右焦点![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上的动点,
是椭圆上的动点,![]() 的最大面积是
的最大面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)圆E经过椭圆的左、右焦点,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,
三点共线,![]() 为坐标原点,直线
为坐标原点,直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,且
,且![]() .
.
(i) 求直线![]() 的斜率;
的斜率;
(ii)当![]() 的面积取到最大值时,求直线
的面积取到最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com