
【题目】(本小题满分12分)已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.

(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)试问:在![]() 轴的正半轴上是否存在一点
轴的正半轴上是否存在一点![]() ,使得
,使得![]() 的外心在
的外心在![]() 上?若存在,求
上?若存在,求![]() 的坐标;若不存在,请说明理由..
的坐标;若不存在,请说明理由..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下结论:
①命题“若![]() ,则
,则![]() ”的逆否命题“若
”的逆否命题“若![]() ,则
,则![]() ”;
”;
②“![]() ”是“
”是“![]() ”的充分条件;
”的充分条件;
③命题“若![]() ,则方程
,则方程![]() 有实根”的逆命题为真命题;
有实根”的逆命题为真命题;
④命题“若![]() ,则
,则![]() 且
且![]() ”的否命题是真命题.
”的否命题是真命题.
其中错误的是__________.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高血压高血糖和高血脂统称“三高”.如图是西南某地区从2010年至2016年患“三高”人数y(单位:千人)的折线图.
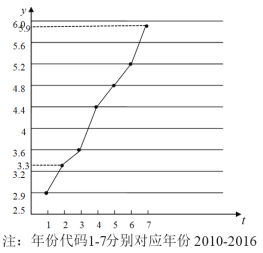
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请求出相关系数(精确到0.01)并加以说明;
的关系,请求出相关系数(精确到0.01)并加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,预测2018年该地区患“三高”的人数.
的回归方程,预测2018年该地区患“三高”的人数.
参考数据:![]() ,
,![]() ,
,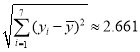 ,
,![]() .参考公式:相关系数
.参考公式:相关系数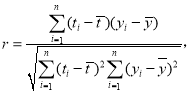 回归方程
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: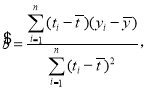
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与直线
与直线![]() 相切且与圆
相切且与圆![]() 外切。
外切。
(1)求圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设第一象限内的点![]() 在轨迹
在轨迹![]() 上,若
上,若![]() 轴上两点
轴上两点![]() ,
,![]() ,满足
,满足![]() 且
且![]() . 延长
. 延长![]() 、
、![]() 分别交轨迹
分别交轨迹![]() 于
于![]() 、
、![]() 两点,若直线
两点,若直线![]() 的斜率
的斜率![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信是腾讯公司推出的一种手机通讯软件,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户为“![]() 组”,否则为“
组”,否则为“![]() 组”,调查结果如下:
组”,调查结果如下:

(1)根据以上数据,能否有60%的把握认为“![]() 组”用户与“性别”有关?
组”用户与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“![]() 组”和“
组”和“![]() 组”的人数;
组”的人数;
(3)从(2)中抽取的5人中再随机抽取3人赠送200元的护肤品套装,记这3人中在“![]() 组”的人数为
组”的人数为![]() ,试求
,试求![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式: 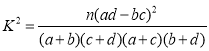 ,其中
,其中![]() .
.
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代劳动人民在筑城、筑堤、挖沟、挖渠、建仓、建囤等工程中,积累了丰富的经验,总结出了一套有关体积、容积计算的方法,这些方法以实际问题的形式被收入我国古代数学名著《九章算术》中.《九章算术·商功》:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”下图解释了这段话中由一个长方体,得到“堑堵”、“阳马”、“鳖臑”的过程.已知堑堵的内切球(与各面均相切)直径为1,则鳖臑的体积最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区观众对大型综艺活动《中国好声音》的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众收看该节目的场数与所对应的人数表:

将收看该节目场次不低于13场的观众称为“歌迷”,已知“歌迷”中有10名女性.
(1)根据已知条件完成下面的2×2列联表
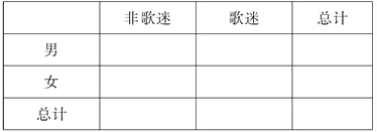
(2)此资料我们能否有95%的把握认为“歌迷”与性别有关?

附: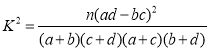
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com