
����Ŀ��ij��ֲ��â���ٽ�����ʱ�������һЩâ������ժ��100��â�����������ֱ���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����λ���ˣ��У���ͳ�Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
����λ���ˣ��У���ͳ�Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
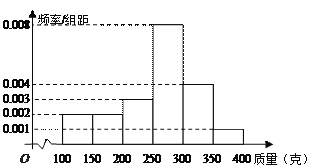
(1) �Թ����������ݵ���������λ����ƽ������
(2)ij���������չ�â�����Ը������ݵ��м��������������ݵ�ƽ��ֵ���������������壬����ֲ�л�δժ�µ�â����Լ����![]() ����������������������չ�������
����������������������չ�������
A������â����![]() Ԫ/ǧ���չ���
Ԫ/ǧ���չ���
B������������![]() �˵�â����
�˵�â����![]() Ԫ/���չ������ڻ����
Ԫ/���չ������ڻ����![]() �˵���
�˵���![]() Ԫ/���չ�.
Ԫ/���չ�.
ͨ������ȷ����ֲѡ�����ַ����������ࣿ
���𰸡���1����������λ����ƽ�����ֱ�Ϊ275;268.75��257.5����2��B����
��������
��1������Ƶ�ʷֲ�ֱ��ͼ���������������λ����������ƽ������
��2���ֱ��������A�ͷ���B�Ļ��������бȽϼ��ɵõ��𰸣�
��1����Ƶ�ʷֲ�ֱ��ͼ������Ϊ��275.
��[100��250����Ƶ��Ϊ��0.002+0.002+0.003����50��0.35��[250��300����Ƶ��Ϊ0.008��50��0.4��
��������������250+![]() ��268.75��
��268.75��
ƽ����Ϊ��![]()
![]() .
.
��2������A��![]() Ԫ.
Ԫ.
����B��������õ���250�ˣ�![]() Ԫ��
Ԫ��
���ڻ����250��![]() Ԫ
Ԫ
�ʵ��ܼ�![]() Ԫ��
Ԫ��
����![]() ����B�����������࣬ӦѡB������
����B�����������࣬ӦѡB������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �IJ���������
�IJ��������� ��
��![]() ����������
Ϊ����������![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ���ᣬ����������ϵ������
���������Ϊ���ᣬ����������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ����ֱ��
����ֱ��![]() ������
������![]() ����
����![]() ����.
����.
������ֱ��![]() ����ͨ���̼�����
����ͨ���̼�����![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
����ֱ��![]() ��
��![]() ��Ľ����Ϊ
��Ľ����Ϊ![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Լ��ˮ���Թ����������л������������ͳ��ij��ͳ�ƾֵ����˸����ڶ��ͥ����ˮ�����������������ˮ����Ƶ�ʷֲ�ֱ��ͼ������ͼ��ʾ��������ˮ����������Ƶ����Ϊ���ʣ�������ÿ�����ˮ���������

��l������δ������3�����������2���µ�����ˮ����������12������1���µ�����ˮ������4�ֵĸ��ʣ�
��2����![]() ��ʾ��δ��3����������ˮ��������12�ֵ�����������軱���
��ʾ��δ��3����������ˮ��������12�ֵ�����������軱���![]() �ķֲ��м���ѧ����
�ķֲ��м���ѧ����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��R��i��������λ������p���ڸ�ƽ���ڣ�����z1=a+ ![]() ��Ӧ�ĵ�λ�ڵڶ����ޣ�����q������z2=a��i��ģ����2����p��q�������⣬��ʵ��a��ֵ���ڣ� ��
��Ӧ�ĵ�λ�ڵڶ����ޣ�����q������z2=a��i��ģ����2����p��q�������⣬��ʵ��a��ֵ���ڣ� ��
A.��1��1
B.![]() ��
�� ![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ����
����
��1��![]() Ϊ
Ϊ![]() �ĵ�����������
�ĵ�����������![]() ����������
����������
��2����![]() ʱ������ʽ
ʱ������ʽ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����ij��Ʒ�ƵĿյ�����ÿ���ܳ�����һ�������Ŀյ������̳�ÿ����һ̨�յ����ɻ���500Ԫ��������������ÿ̨����Ŀյ����轻���ܷ�100Ԫ��������Ӧ����ɴ������̵������Ӧ����ʱÿ̨�յ�����������200Ԫ�� ���������̳��ܳ�����20̨�յ��������ܵ�����λ��Ԫ�����ڵ���������n����λ��̨��n��N���ĺ�������ʽf��n����
�����̳���¼��ȥ�����죨��10�ܣ��յ���������n����λ��̨���������ñ���
��������n | 18 | 19 | 20 | 21 | 22 |
Ƶ�� | 1 | 2 | 3 | 3 | 1 |
��10�ܼ�¼�ĸ���������Ƶ����Ϊ�������������ĸ��ʣ����̳��ܳ�����20̨�յ�����X��ʾ���ܵ�����λ��Ԫ������X�ķֲ��м���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻҩ������IJ�����![]() ��һ����Χ�ڵ��¶�
��һ����Χ�ڵ��¶�![]() �йأ����ռ��˸���ҩ�������6��۲��������±���
�йأ����ռ��˸���ҩ�������6��۲��������±���
�¶� | 21 | 23 | 24 | 27 | 29 | 32 |
������ | 6 | 11 | 20 | 27 | 57 | 77 |
��1���������Իع�ģ�ͣ���![]() ����
����![]() �Ļع鷽��
�Ļع鷽��![]() ����ȷ��0.1����
����ȷ��0.1����
��2�����÷����Իع�ģ����![]() ��
��![]() �Ļع鷽��Ϊ
�Ļع鷽��Ϊ![]() �������ָ��
�������ָ��![]()
�����루1���е����Իع�ģ����ȣ���![]() ˵������ģ�͵����Ч������.
˵������ģ�͵����Ч������.
�������Ч���õ�ģ��Ԥ���¶�Ϊ![]() ʱ����ҩ������IJ����������ȡ������.
ʱ����ҩ������IJ����������ȡ������.
����һ������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹���Ϊ
��б�ʺͽؾ����С���˹���Ϊ �����ָ��
�����ָ�� .
.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�� ![]() =����
=���� ![]() sin��x��cos��x����
sin��x��cos��x���� ![]() =��cos��x��cos��x�����أ�0���Ǻ���f��x��=
=��cos��x��cos��x�����أ�0���Ǻ���f��x��= ![]()
![]() ����f��x������С������Ϊ�У�
����f��x������С������Ϊ�У�
��1����ص�ֵ��
��2����f��x���ĵ����ݼ����䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��
��1����ֱ��![]() ��Բ
��Բ![]() �صõ��ҳ�Ϊ
�صõ��ҳ�Ϊ![]() ����ʵ��
����ʵ��![]() ��ֵ��
��ֵ��
��2����![]() ʱ����ֱ��
ʱ����ֱ��![]() �ϵĶ���
�ϵĶ���![]() ��Բ
��Բ![]() ���������ߣ����е�ֱ�Ϊ
���������ߣ����е�ֱ�Ϊ![]() ��
��![]() ������ֱ��
������ֱ��![]() ���Ƿ����һ�����㣿�����ڣ�����ö�������ꣻ�������ڣ���˵�����ɣ�
���Ƿ����һ�����㣿�����ڣ�����ö�������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com