
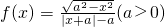 ,既不是奇函数,又不是偶函数;
,既不是奇函数,又不是偶函数;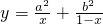 的最小值是a2+b2;
的最小值是a2+b2;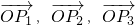 满足条件
满足条件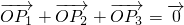 ,且
,且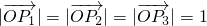 ,则△P1P2P3为正三角形;
,则△P1P2P3为正三角形;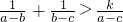 恒成立,则k∈(0,2);
恒成立,则k∈(0,2);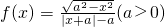 的定义域,为[-a,a],∴f(x)可化简为f(x)=
的定义域,为[-a,a],∴f(x)可化简为f(x)=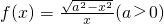
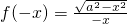 =-f(x),∴函数
=-f(x),∴函数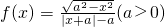 为奇函数,(1)错误.
为奇函数,(1)错误.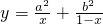 的函数值不可能等于a2+b2,∴(2)错误.
的函数值不可能等于a2+b2,∴(2)错误.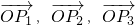 满足条件
满足条件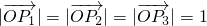 ,
,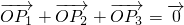 ,
,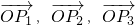 ,任两个所成角都为120°,
,任两个所成角都为120°,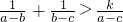 可变形为k<
可变形为k<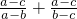 ,
,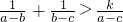 恒成立,则k一定小于
恒成立,则k一定小于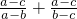 的最小值,
的最小值,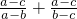 =
=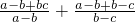 =
=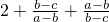 ≥4,∴k∈(-∞,40,∴(4)错误
≥4,∴k∈(-∞,40,∴(4)错误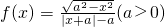 的奇偶性,先求函数的定义域,再化简函数,最后计算f(-x),与f(x)比较即可.
的奇偶性,先求函数的定义域,再化简函数,最后计算f(-x),与f(x)比较即可.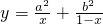 的函数值一定大于a2+b2,所以函数
的函数值一定大于a2+b2,所以函数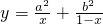 的最小值不是a2+b2.
的最小值不是a2+b2.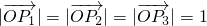 判断点P1,P2,P3都在以O为圆心,半径是1的圆上,再根据
判断点P1,P2,P3都在以O为圆心,半径是1的圆上,再根据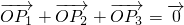 ,判断三个向量
,判断三个向量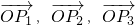 ,任两个所成角都为120°,就可金额得到∴△P1P2P3为正三角形.
,任两个所成角都为120°,就可金额得到∴△P1P2P3为正三角形.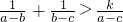 变形为k<
变形为k<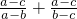 ,借助均值定理求出k的范围,与所给范围比较即可.
,借助均值定理求出k的范围,与所给范围比较即可.

 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2+4 | ||
|
| x2 |
| 9 |
| x |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com