
 ;(Ⅱ)从第3年开始盈利;(Ⅲ)方案Ⅰ比较合理.
;(Ⅱ)从第3年开始盈利;(Ⅲ)方案Ⅰ比较合理. ,每年支付的维修保养费用构成一等差数列,由等差数列求和公式可得使用x年的总支出,总收入减去总支出便可得使用x年后数控机床的盈利额,从而得y与x之间的函数关系式.
,每年支付的维修保养费用构成一等差数列,由等差数列求和公式可得使用x年的总支出,总收入减去总支出便可得使用x年后数控机床的盈利额,从而得y与x之间的函数关系式. 便可得
便可得 的范围,从而知道从从第几年开始盈利.
的范围,从而知道从从第几年开始盈利.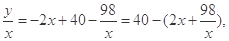
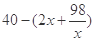 可用重要不等式求出其最大值,从而可确定什么时候年平均盈利额达到最大值,可求出工厂获得的总利润.
可用重要不等式求出其最大值,从而可确定什么时候年平均盈利额达到最大值,可求出工厂获得的总利润.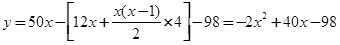 (x
(x N*). 3分
N*). 3分 得
得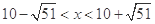 .
.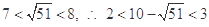 .又∵x
.又∵x N*,∴3≤x≤17,故从第3年开始盈利. 7分
N*,∴3≤x≤17,故从第3年开始盈利. 7分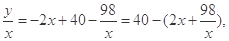
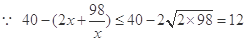 ,当且仅当
,当且仅当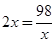 时,即x=7时等号成立.
时,即x=7时等号成立.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
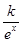 (e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元. 为常数
为常数 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
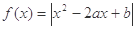
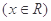 ,给出下列命题:
,给出下列命题: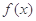 必是偶函数;
必是偶函数;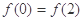 时,
时,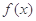 的图象关于直线
的图象关于直线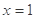 对称;
对称;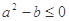 ,则
,则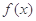 在区间
在区间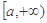 上是增函数;
上是增函数;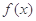 有最大值
有最大值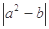 .
. | A.(3) | B.(2)(3) | C.(3)(4) | D.(1)(2)(3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com