
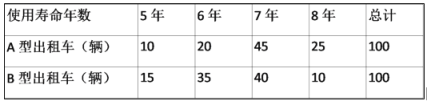
【题目】2020年春季,某出租汽车公同决定更换一批新的小汽车以代替原来报废的出租车,现有采购成本分别为11万元/辆和8万元/辆的A,B两款车型,根据以往这两种出租车车型的数据,得到两款出租车型使用寿命频数表如表:
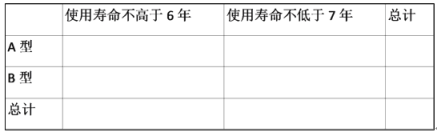
(1)填写如表,并判断是否有99%的把握认为出租车的使用寿命年数与汽车车有关?
(2)以频率估计概率,从2020年生产的A和B的车型中各随机抽1车,以X表示这2车中使用寿命不低于7年的车数,求X的分布列和数学期望;
(3)根据公司要求,采购成本由出租公司负责,平均每辆出租每年上交公司6万元,其余维修和保险等费用自理,假设每辆出租车的使用寿命都是整数年,用频率估计每辆出租车使用寿命的概率,分别以这100辆出租车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择采购哪款车型?
参考公式: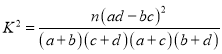 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
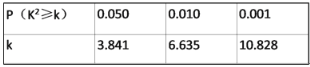
【答案】(1)填表见解析;有99%的把握认为出租车的使用寿命年数与汽车车有关(2)详见解析(3)会选择采购B款车型
【解析】
(1)先补充完整2×2列联表,然后根据K2的公式计算出其观测值,并与附表中的数据进行对比即可作出判断;
(2)X的可能取值为0,1,2,先求出两种车型使用寿命不低于7年和低于7年的占比数,然后依据相互独立事件的概率逐一求出每个X的取值所对应的概率即可得分布列,进而求得数学期望;
(3)先求出两款出租车型的每辆车的利润,然后结合频数分布列求两种车型的平均利润,比较大小后,取较大者即可.
(1)补充完整的2×2列联表如下所示:
使用寿命 | 使用寿命不高于6年 | 使用寿命不低于7年 | 总 计 |
A型 | 30 | 70 | 100 |
B型 | 50 | 50 | 100 |
总计 | 80 | 120 | 200 |
∴![]() ,
,
∴有99%的把握认为出租车的使用寿命年数与汽车车型有关;
(2)由题可知,A型车使用寿命不低于7年的车数占![]() ,低于7年的车数占
,低于7年的车数占![]() ;
;
B型车使用寿命不低于7年的车数占![]() ,低于7年的车数占
,低于7年的车数占![]() ,
,
∴X的可能取值为0,1,2,
![]() ,
,![]() ,
,
![]() ,
,
∴X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
∴![]() ;
;
(3)∵平均每辆出租车年上交公司6万元,且A,B两款车型的采购成本分别为11万元/辆和8万元/辆,
∴两款出租车型的每辆车的利润如下表:
使用寿命 | 5年 | 6年 | 7年 | 8年 |
A型 |
|
|
|
|
B型 |
|
|
|
|
用频率估计概率,这100辆A型出租车的平均利润为:![]() (万元),
(万元),
这100辆B型出租车的平均利润为:
![]() (万元),
(万元),
∵30.7>30.1,
故会选择采购B款车型.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣sinx(a∈R).
(1)当![]() 时,f(x)
时,f(x)![]() 0恒成立,求正实数a的取值范围;
0恒成立,求正实数a的取值范围;
(2)当a≥1时,探索函数F(x)![]() f(x)﹣cosx+a﹣1在(0,π)上的零点个数,并说明理由.
f(x)﹣cosx+a﹣1在(0,π)上的零点个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,港口A在港口O的正东100海里处,在北偏东方向有条直线航道OD,航道和正东方向之间有一片以B为圆心,半径为![]() 海里的圆形暗礁群(在这片海域行船有触礁危险),其中OB=
海里的圆形暗礁群(在这片海域行船有触礁危险),其中OB=![]() 海里,tan∠AOB=
海里,tan∠AOB=![]() ,cos∠AOD=
,cos∠AOD=![]() ,现一艘科考船以
,现一艘科考船以![]() 海里/小时的速度从O出发沿OD方向行驶,经过2个小时后,一艘快艇以50海里/小时的速度准备从港口A出发,并沿直线方向行驶与科考船恰好相遇.
海里/小时的速度从O出发沿OD方向行驶,经过2个小时后,一艘快艇以50海里/小时的速度准备从港口A出发,并沿直线方向行驶与科考船恰好相遇.
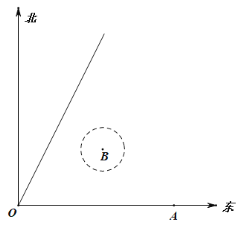
(1)若快艇立即出发,判断快艇是否有触礁的危险,并说明理由;
(2)在无触礁危险的情况下,若快艇再等x小时出发,求x的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过椭圆
过椭圆![]() 的左、右焦点
的左、右焦点![]() 和短轴的端点
和短轴的端点![]() (点
(点![]() 在点
在点![]() 上方).
上方).![]() 为圆
为圆![]() 上的动点(点
上的动点(点![]() 不与
不与![]() 重合),直线
重合),直线![]() 分别与椭圆交于点
分别与椭圆交于点![]() ,其中点
,其中点![]() 构成四边形.
构成四边形.
(1)求椭圆的标准方程;
(2)求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点纵坐标伸长到原来的
上各点纵坐标伸长到原来的![]() 倍(横坐标不变),得到曲线
倍(横坐标不变),得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 上是否存在不同的两点
上是否存在不同的两点![]() ,
,![]() (以上两点坐标均为极坐标,
(以上两点坐标均为极坐标,![]() ,
,![]() ,
,![]() ,
,![]() ),使点
),使点![]() 、
、![]() 到
到![]() 的距离都为
的距离都为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“克拉茨猜想”又称“![]() 猜想”,是德国数学家洛萨克拉茨在
猜想”,是德国数学家洛萨克拉茨在![]() 年世界数学家大会上公布的一个猜想:任给一个正整数
年世界数学家大会上公布的一个猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半;如果
是偶数,就将它减半;如果![]() 为奇数就将它乘
为奇数就将它乘![]() 加
加![]() ,不断重复这样的运算,经过有限步后,最终都能够得到
,不断重复这样的运算,经过有限步后,最终都能够得到![]() ,得到
,得到![]() 即终止运算,己知正整数
即终止运算,己知正整数![]() 经过
经过![]() 次运算后得到
次运算后得到![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() D.
D.![]() 或
或![]() 或
或![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,我国突发新冠肺炎疫情,疫情期间中小学生“停课不停学”.已知某地区中小学生人数情况如甲图所示,各学段学生在疫情期间“家务劳动”的参与率如乙图所示.为了进一步了解该地区中小学生参与“家务劳动”的情况,现用分层抽样的方法抽取4%小学初中高中学段的学生进行调查,则抽取的样本容量、抽取的高中生家中参与“家务劳动”的人数分别为( )
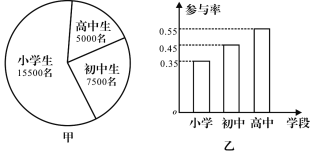
A.2750,200B.2750,110C.1120,110D.1120,200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为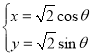 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为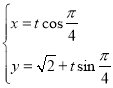 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求曲线![]() 与曲线
与曲线![]() 的公共点的极坐标;
的公共点的极坐标;
(2)若点![]() 的极坐标为
的极坐标为![]() ,设曲线
,设曲线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,则在曲线
,则在曲线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的直角坐标,若不存在,请说明理由.
的直角坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研团队对![]() 例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中
例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中![]() 名吸烟患者中,重症人数为
名吸烟患者中,重症人数为![]() 人,重症比例约为
人,重症比例约为![]() ;
;![]() 名非吸烟患者中,重症人数为
名非吸烟患者中,重症人数为![]() 人,重症比例为
人,重症比例为![]() .
.
(1)根据以上数据完成![]() 列联表;
列联表;
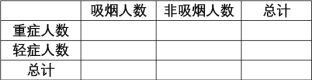
(2)根据(1)中列联表数据,能否在犯错误的概率不超过![]() 的前提下认为新冠肺炎重症与吸烟有关?
的前提下认为新冠肺炎重症与吸烟有关?
(3)已知每例重症患者平均治疗费用约为![]() 万元,每例轻症患者平均治疗费用约为
万元,每例轻症患者平均治疗费用约为![]() 万元.根据(1)中列联表数据,分别求吸烟患者和非吸烟患者的平均治疗费用.(结果保留两位小数)
万元.根据(1)中列联表数据,分别求吸烟患者和非吸烟患者的平均治疗费用.(结果保留两位小数)
附:
|
|
|
|
|
|
|
|
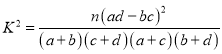
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com