
【题目】在![]() 的表格填上数字,设在第i行第j列所组成的数字为
的表格填上数字,设在第i行第j列所组成的数字为![]() ,
,![]() ,
,![]() ,则表格中共有5个1的填表方法种数为______.
,则表格中共有5个1的填表方法种数为______.
【答案】326
【解析】
根据题意,按数字1出现的位置分三种情况讨论,![]() 、5个1都出现在
、5个1都出现在![]() 即
即![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这5个表格中,
这5个表格中,![]() 、有1个1出现在
、有1个1出现在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这5个表格中,剩余4个1在其他位置,
这5个表格中,剩余4个1在其他位置,![]() 、有3个1出现在
、有3个1出现在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这5个表格中,剩余2个1在其他位置,分别求出每种情况下填表方法的数目,进而由分类计数原理计算可得答案.
这5个表格中,剩余2个1在其他位置,分别求出每种情况下填表方法的数目,进而由分类计数原理计算可得答案.
解:根据题意,在![]() 的表格中,有5个
的表格中,有5个![]() 的表格,即
的表格,即![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,10个
,10个![]() 的表格,10个
的表格,10个![]() 的表格;
的表格;
要求![]() 的表格种恰有5个1,则对1出现的位置分3种情况讨论:
的表格种恰有5个1,则对1出现的位置分3种情况讨论:
![]() 、5个1都出现在
、5个1都出现在![]() 即
即![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这5个表格中,有1种情况;
这5个表格中,有1种情况;
![]() 、有1个1出现在
、有1个1出现在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这5个表格中,剩余4个1在其他位置,
这5个表格中,剩余4个1在其他位置,
需要先在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这5个表格中,选出1个,有
这5个表格中,选出1个,有![]() 种情况,
种情况,
在剩下的10个![]() 表格中,任选2个,有
表格中,任选2个,有![]() 种情况,
种情况,
则有![]() 种填表方法;
种填表方法;
![]() 、有3个1出现在
、有3个1出现在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这5个表格中,剩余2个1在其他位置,
这5个表格中,剩余2个1在其他位置,
需要先在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这5个表格中,选出3个,有
这5个表格中,选出3个,有![]() 种情况,
种情况,
在剩下的10个![]() 表格中,任选1个,有
表格中,任选1个,有![]() 种情况,
种情况,
则有![]() 种填表方法;
种填表方法;
则一共有![]() 种填表方法;
种填表方法;
故答案为:326.


科目:高中数学 来源: 题型:
【题目】如图,地图上有一竖直放置的圆形标志物,圆心为C,与地面的接触点为G.与圆形标志物在同一平面内的地面上点P处有一个观测点,且PG=50m.在观测点正前方10m处(即PD=10m)有一个高位10m(即ED=10m)的广告牌遮住了视线,因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧.

(1)若圆形标志物半径为25m,以PG所在直线为X轴,G为坐标原点,建立直角坐标系,求圆C和直线PF的方程;
(2)若在点P处观测该圆形标志的最大视角(即![]() )的正切值为
)的正切值为![]() ,求该圆形标志物的半径.
,求该圆形标志物的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 是双曲线
是双曲线![]() :
:![]() (
(![]() ,
,![]() )的两个顶点,点
)的两个顶点,点![]() 是双曲线上异于
是双曲线上异于![]() 、
、![]() 的一点,
的一点,![]() 为坐标原点,射线
为坐标原点,射线![]() 交椭圆
交椭圆![]() :
:![]() 于点
于点![]() ,设直线
,设直线![]() 、
、![]() 、
、![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() 、
、![]() 、
、![]() .
.
(1)若双曲线![]() 的渐近线方程是
的渐近线方程是![]() ,且过点
,且过点![]() ,求
,求![]() 的方程;
的方程;
(2)在(1)的条件下,如果![]() ,求△
,求△![]() 的面积;
的面积;
(3)试问:![]() 是否为定值?如果是,请求出此定值;如果不是,请说明理由.
是否为定值?如果是,请求出此定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() (点
(点![]() 在
在![]() 轴上方),斜率为
轴上方),斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,且
,且![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)设椭圆![]() 的离心率为
的离心率为![]() ,当点
,当点![]() 为椭圆
为椭圆![]() 的右顶点时,
的右顶点时,![]() 的坐标为
的坐标为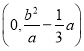 ,求
,求![]() 的值.
的值.
(2)若椭圆![]() 的方程为
的方程为![]() ,且
,且![]() ,是否存
,是否存![]() 在使得
在使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 是双曲线
是双曲线![]() 的两个顶点,点
的两个顶点,点![]() 是双曲线上异于
是双曲线上异于![]() 、
、![]() 的一点,
的一点,![]() 为坐标原点,射线
为坐标原点,射线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,设直线
,设直线![]() 、
、![]() 、
、![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() 、
、![]() 、
、![]() .
.
(1)若双曲线![]() 的渐近线方程是
的渐近线方程是![]() ,且过点
,且过点![]() ,求
,求![]() 的方程;
的方程;
(2)在(1)的条件下,如果![]() ,求
,求![]() 的面积;
的面积;
(3)试问:![]() 是否为定值?如果是,请求出此定值;如果不是,请说明理由.
是否为定值?如果是,请求出此定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二理科1班共有50名学生参加学业水平模拟考试,成绩(单位:分,满分100分)大于或等于90分的为优秀,其中语文成绩近似服从正态分布![]() ,数学成绩的频率分布直方图如图.
,数学成绩的频率分布直方图如图.
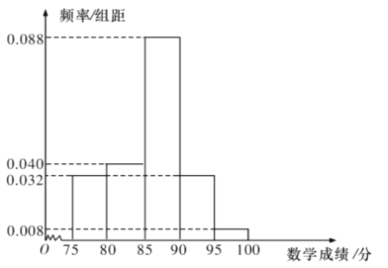
(1)这50名学生中本次考试语文、数学成绩优秀的大约各有多少人?
(2)如果语文和数学两科成绩都优秀的共有4人,从语文优秀或数学优秀的这些同学中随机抽取3人,设3人中两科都优秀的有X人,求X的分布列和数学期望;
(3)根据(1)(2)的数据,是否有99%以上的把握认为语文成绩优秀的同学,数学成绩也优秀?
语文优秀 | 语文不优秀 | 合计 | |
数学优秀 | |||
数学不优秀 | |||
合计 |
附:①若![]() ,则
,则![]() ,
,![]() ;②
;②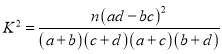 ;
;
③
| 0.1 | 0.05 | 0.025 | 0.010 | p>0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数![]() ,
,![]() ,对于定义在
,对于定义在![]() 上的函数
上的函数![]() ,有下述命题:
,有下述命题:
①“![]() 是奇函数”的充要条件是“函数
是奇函数”的充要条件是“函数![]() 的图像关于点
的图像关于点![]() 对称”;
对称”;
②“![]() 是偶函数”的充要条件是“函数
是偶函数”的充要条件是“函数![]() 的图像关于直线
的图像关于直线![]() 对称”;
对称”;
③“![]() 是
是![]() 的一个周期”的充要条件是“对任意的
的一个周期”的充要条件是“对任意的![]() ,都有
,都有![]() ”;
”;
④“函数![]() 与
与![]() 的图像关于
的图像关于![]() 轴对称”的充要条件是“
轴对称”的充要条件是“![]() ”
”
其中正确命题的序号是( )
A.①②B.②③C.①④D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com