
【题目】定义:若函数![]() 对任意的
对任意的![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 为
为![]() 上的“淡泊”函数.
上的“淡泊”函数.
(1)判断![]() 是否为
是否为![]() 上的“淡泊”函数,说明理由;
上的“淡泊”函数,说明理由;
(2)是否存在实数![]() ,使
,使![]() 为
为![]() 上的“淡泊”函数,若存在,求出
上的“淡泊”函数,若存在,求出![]() 的取值范围;不存在,说明理由;
的取值范围;不存在,说明理由;
(3)设![]() 是
是![]() 上的“淡泊”函数(其中
上的“淡泊”函数(其中![]() 不是常值函数),且
不是常值函数),且![]() ,若对任意的
,若对任意的![]() ,都有
,都有![]() 成立,求
成立,求![]() 的最小值.
的最小值.
【答案】(1)是,理由详见解析;(2)存在,![]() ;(3)最小值为
;(3)最小值为![]() .
.
【解析】
(1)任取x1,x2∈[﹣1,1],可得|f(x1)﹣f(x2)|的不等式,结合题意可判函数为“淡泊”函数;
(2)假设存在k∈R,使得![]() 在[﹣1,+∞)上为“淡泊”函数,则满足对任意x1,x2∈[﹣1,+∞),都有|f(x1)﹣f(x2)|≤|x1﹣x2|成立,代入已知可得k的不等式,解不等式可得;
在[﹣1,+∞)上为“淡泊”函数,则满足对任意x1,x2∈[﹣1,+∞),都有|f(x1)﹣f(x2)|≤|x1﹣x2|成立,代入已知可得k的不等式,解不等式可得;
(3)不妨令0<x1≤x2<1,运用绝对值不等式的性质以及新定义,即可得到结论.
(1)任取x1,x2∈[﹣1,1],可得|f(x1)﹣f(x2)|
=|(![]() )﹣(
)﹣(![]() )|
)|
=|![]() (x1+x2)(x1﹣x2)
(x1+x2)(x1﹣x2)![]() (x1﹣x2)|
(x1﹣x2)|
=|x1﹣x2||![]() (x1+x2)
(x1+x2)![]() |
|
∵x1,x2∈[﹣1,1],∴![]() (x1+x2)∈[
(x1+x2)∈[![]() ,
,![]() ],
],
∴![]() (x1+x2)
(x1+x2)![]() |∈[0,1],即|
|∈[0,1],即|![]() (x1+x2)
(x1+x2)![]() |≤1,
|≤1,
∴|x1﹣x2||![]() (x1+x2)
(x1+x2)![]() |≤|x1﹣x2|
|≤|x1﹣x2|
∴|f(x1)﹣f(x2)|≤|x1﹣x2|
∴函数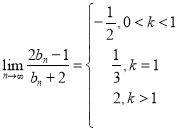 在[﹣1,1]上是“淡泊”函数;
在[﹣1,1]上是“淡泊”函数;
(2)假设存在k∈R,使得![]() 在[﹣1,+∞)上为“淡泊”函数,
在[﹣1,+∞)上为“淡泊”函数,
则满足对任意x1,x2∈[﹣1,+∞),都有|f(x1)﹣f(x2)|≤|x1﹣x2|成立,
故|![]() |=|k||
|=|k||![]() |≤|x1﹣x2|,
|≤|x1﹣x2|,
∴|k|≤|(x1+2)(x2+2)|,
∵x1,x2∈[﹣1,+∞),∴(x1+2)(x2+2)>1,
∴|k|≤1,解得﹣1≤k≤1;
(3)不妨令0<x1≤x2<1,由“淡泊”函数性质,有|f(x1)﹣f(x2)|≤|x1﹣x2|成立,
若x2﹣x1![]() ,则|f(x1)﹣f(x2)|≤|x1﹣x2|
,则|f(x1)﹣f(x2)|≤|x1﹣x2|![]() ;
;
若x2﹣x1![]() ,|f(x1)﹣f(x2)|=|f(x1)﹣f(0)+f(1)﹣f(x2)|
,|f(x1)﹣f(x2)|=|f(x1)﹣f(0)+f(1)﹣f(x2)|
≤|f(x1)﹣f(0)|+|f(1)﹣f(x2)|≤|x1﹣0|+|1﹣x2|=1﹣x2+x1=1﹣(x2﹣x1)![]() ,
,
综上,对任意0<x1≤x2<1,|f(x1)﹣f(x2)|![]() 恒成立,
恒成立,
而![]() 对任意的
对任意的![]() ,都成立,则
,都成立,则![]()
![]()
∴![]() ,即
,即![]() 的最小值为
的最小值为![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】![]() 统计学中将
统计学中将![]() 个数
个数![]() 的和记作
的和记作![]()
(1)设![]()
![]() ,求
,求![]() ;
;
(2)是否存在互不相等的非负整数![]() ,
,![]() ,使得
,使得![]() 成立,若存在,请写出推理的过程;若不存在请证明;
成立,若存在,请写出推理的过程;若不存在请证明;
(3)设![]()
![]() 是不同的正实数,
是不同的正实数,![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,判断
,判断![]() 是否为一个等比数列,请说明理由.
是否为一个等比数列,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,如果存在两条平行直线
,如果存在两条平行直线![]() 与
与![]()
![]() ,使得对于任意
,使得对于任意![]() ,都有
,都有![]() 恒成立,那么称函数
恒成立,那么称函数![]() 是带状函数,若
是带状函数,若![]() ,
,![]() 之间的最小距离
之间的最小距离![]() 存在,则称
存在,则称![]() 为带宽.
为带宽.
(1)判断函数![]() 是不是带状函数?如果是,指出带宽(不用证明);如果不是,说明理由;
是不是带状函数?如果是,指出带宽(不用证明);如果不是,说明理由;
(2)求证:函数![]() (
(![]() )是带状函数;
)是带状函数;
(3)求证:函数![]() (
(![]() )为带状函数的充要条件是
)为带状函数的充要条件是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社会机构为了调查对手机游戏的兴趣与年龄的关系,通过问卷调查,整理数据得如下![]() 列联表:
列联表:

(1)根据列联表,能否有![]() 的把握认为对手机游戏的兴趣程度与年龄有关?
的把握认为对手机游戏的兴趣程度与年龄有关?
(2)若已经从40岁以上的被调查者中用分层抽样的方式抽取了10名,现从这10名被调查者中随机选取3名,记这3名被选出的被调查者中对手机游戏很有兴趣的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:![]()
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 过点
过点![]() ,且渐近线方程为
,且渐近线方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于点
交于点![]() 、
、![]() 两点.
两点.
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() 过原点,点
过原点,点![]() 是曲线
是曲线![]() 上任一点,直线
上任一点,直线![]() ,
,![]() 的斜率都存在,记为
的斜率都存在,记为![]() 、
、![]() ,试探究
,试探究![]() 的值是否与点
的值是否与点![]() 及直线
及直线![]() 有关,并证明你的结论;
有关,并证明你的结论;
(3)若直线![]() 过点
过点![]() ,问在
,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为常数?若存在,求出点
为常数?若存在,求出点![]() 坐标及此常数的值;若不存在,说明理由.
坐标及此常数的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场营销人员进行某商品M市场营销调查发现,每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过试点统计得到以下表:
反馈点数 | 1 | 2 | 3 | 4 | 5 |
销量(百件)/天 | 0. 5 | 0. 6 | 1 | 1. 4 | 1. 7 |
(1)经分析发现,可用线性回归模型拟合当地该商品销量![]() (百件)与返还点数
(百件)与返还点数![]() 之间的相关关系. 请用最小二乘法求
之间的相关关系. 请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测若返回6个点时该商品每天销量;
,并预测若返回6个点时该商品每天销量;
(2)若节日期间营销部对商品进行新一轮调整. 已知某地拟购买该商品的消费群体十分庞大,经营销调研机构对其中的200名消费者的返点数额的心理预期值进行了一个抽样调查,得到如下一份频数表:
返还点数预期值区间(百分比) |
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
(ⅰ)求这200位拟购买该商品的消费者对返点点数的心理预期值![]() 的样本平均数及中位数的估计值(同一区间的预期值可用该区间的中点值代替;估计值精确到0. 1);
的样本平均数及中位数的估计值(同一区间的预期值可用该区间的中点值代替;估计值精确到0. 1);
(ⅱ)将对返点点数的心理预期值在![]() 和
和![]() 的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取2名进行跟踪调查,设抽出的2人中,至少有一个人是“欲望膨胀型”消费者的概率是多少?
的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取2名进行跟踪调查,设抽出的2人中,至少有一个人是“欲望膨胀型”消费者的概率是多少?
参考公式及数据:①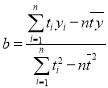 ,
,![]() ;②
;②![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com