
【题目】已知函数g(x)=x+ ![]() ﹣2.
﹣2.
(1)证明:函数g(x)在[ ![]() ,+∞)上是增函数;
,+∞)上是增函数;
(2)若不等式g(2x)﹣k2x≥0在x∈[﹣1,1]上有解,求实数k的取值范围.
【答案】
(1)证明:设 ![]() ≤x1<x2,
≤x1<x2,
∵g(x1)﹣g(x2)= ![]() ,
,
∵ ![]() ≤x1<x2,∴x1﹣x2<0,2<x1x2,即x1x2﹣2>0.
≤x1<x2,∴x1﹣x2<0,2<x1x2,即x1x2﹣2>0.
∴g(x1)﹣g(x2)<0,即g(x1)<g(x2),
所以函数g(x)在[ ![]() ,+∞)上是增函数
,+∞)上是增函数
(2)解:g(2x)﹣k2x≥0,可化为2x+ ![]() ﹣2≥k2x,
﹣2≥k2x,
化为1+2 ![]() ﹣2
﹣2 ![]() ≥k,
≥k,
令t= ![]() ,则k≤2t2﹣2t+1,
,则k≤2t2﹣2t+1,
因x∈[﹣1,1],故t∈[ ![]() ,2],
,2],
记h(t)=2t2﹣2t+1,因为t∈[ ![]() ,2],故h(t)max=5,
,2],故h(t)max=5,
所以k的取值范围是(﹣∞,5]
【解析】(1)根据函数单调性的定义证明即可;(2)问题化为1+2 ![]() ﹣2
﹣2 ![]() ≥k,令t=
≥k,令t= ![]() ,则k≤2t2﹣2t+1,从而求出k的范围即可.
,则k≤2t2﹣2t+1,从而求出k的范围即可.
【考点精析】通过灵活运用函数单调性的判断方法,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,(a>0).
,(a>0).
(1)当a=2时,证明函数f(x)不是奇函数;
(2)判断函数f(x)的单调性,并利用函数单调性的定义给出证明;
(3)若f(x)是奇函数,且f(x)﹣x2+4x≥m在x∈[﹣2,2]时恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在x=1处的切线与直线
在x=1处的切线与直线![]() 平行。
平行。
(Ⅰ)求a的值并讨论函数y=f(x)在![]() 上的单调性。
上的单调性。
(Ⅱ)若函数![]() (
(![]() 为常数)有两个零点
为常数)有两个零点![]() ,
,
(1)求m的取值范围;
(2)求证: ![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求曲线![]() 的直角坐标方程,并指出其表示何种曲线;
的直角坐标方程,并指出其表示何种曲线;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的直角坐标为
的直角坐标为![]() ,
,
试求当![]() 时,
时, ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】漳州水仙鳞茎硕大,箭多花繁,色美香郁,素雅娟丽,有“天下水仙数漳州”之美誉.现某水仙花雕刻师受雇每天雕刻250粒水仙花,雕刻师每雕刻一粒可赚1.2元,如果雕刻师当天超额完成任务,则超出的部分每粒多赚0.5元;如果当天未能按量完成任务,则按完成的雕刻量领取当天工资.
(Ⅰ)求雕刻师当天收入(单位:元)关于雕刻量![]() (单位:粒,
(单位:粒, ![]() )的函数解析式
)的函数解析式![]() ;
;
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量![]() (单位:粒),整理得下表:
(单位:粒),整理得下表:
雕刻量 | 210 | 230 | 250 | 270 | 300 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10天记录的各雕刻量的频率作为各雕刻量发生的概率.
(ⅰ)求该雕刻师这10天的平均收入;
(ⅱ)求该雕刻师当天的收入不低于300元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学一位高三班主任对本班50名学生学习积极性和对班级工作的态度进行调查, 得倒的统计数据如表所示:
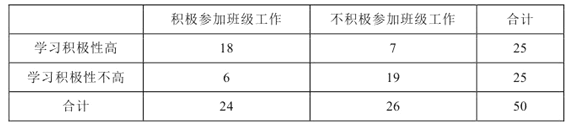
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作的且学习积极性高的7名学生中有两名男生,现从中抽取2名学生参加某项活动,问2名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com