
����Ŀ��Ϊ���о������Ϻ��̲���ʧ�ߡ�����ϵ��������100����ʿ���õ��������������
ʧ�� | ��ʧ�� | �ϼ� | |
���Ϻ��̲� | 16 | 40 | 56 |
���ϲ����̲� | 5 | 39 | 44 |
�ϼ� | 21 | 79 | 100 |
����֪���ݿ�����ã�![]() ������������ٽ�ֵ����
������������ٽ�ֵ����
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
���������Ľ����ǣ� ��
A. �ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ�����Ϻ��̲���ʧ���йء�
B. �ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ�����Ϻ��̲���ʧ���ء�
C. �ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ�����Ϻ��̲���ʧ���йء�
D. �ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ�����Ϻ��̲���ʧ���ء�
 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() ��ͼ����ͼ��ʾ��
��ͼ����ͼ��ʾ��
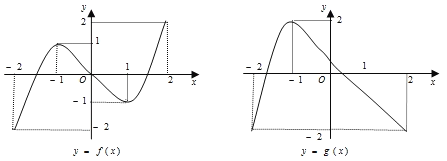
���������ĸ����⣺
(1)����![]() ���ҽ���6������
���ҽ���6������
(2)����![]() ���ҽ���3������
���ҽ���3������
(3)����![]() ���ҽ���5������
���ҽ���5������
(4)����![]() ���ҽ���4������
���ҽ���4������
������ȷ����ĸ�����( )
A. 4��B. 3��C. 2��D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ����C�ǰ�ԲO�ϳ�A��B���һ�����㣬DC��ֱ�ڰ�ԲO���ڵ�ƽ�棬DC��EB��DC=EB��AB=4��tan��EAB=![]() ��
��
֤����ƽ��ADE��ƽ��ACD.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������У���������![]() ��(3��2)��ʾ��������(�� ��)
��(3��2)��ʾ��������(�� ��)
A. ![]() ��(0��0)��
��(0��0)��![]() ��(1��2)B.
��(1��2)B. ![]() ��(��1��2)��
��(��1��2)��![]() ��(5����2)
��(5����2)
C. ![]() ��(3��5)��
��(3��5)��![]() ��(6��10)D.
��(6��10)D. ![]() ��(2����3)��
��(2����3)��![]() ��(��2��3)
��(��2��3)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn �� a1=1����nan+1=2Sn��n��N*��������{bn}����b1=![]() �� b2=
�� b2=![]() �� ������n��N* �� ����bn+12=bnbn+2 ��
�� ������n��N* �� ����bn+12=bnbn+2 ��
������{an}��{bn}��ͨ�ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ǵ¹���ѧ�ң�����1937�������һ�������IJ��룺�θ�һ��������![]() �����
�����![]() ��ż�����ͽ������루��
��ż�����ͽ������루��![]() �������
�������![]() ��������������3��1����
��������������3��1����![]() ���������ظ����������㣬����������һ�����Եõ�1�����ʼ������Ϊ6�����������任�������ǵõ�һ�����У�6,3,10,5,16,8,4,2,1.�Կ����IJ��룬Ŀǰ˭Ҳ����֤���������ܷ������������
���������ظ����������㣬����������һ�����Եõ�1�����ʼ������Ϊ6�����������任�������ǵõ�һ�����У�6,3,10,5,16,8,4,2,1.�Կ����IJ��룬Ŀǰ˭Ҳ����֤���������ܷ������������![]() ������������ʵʩ�任��ע��1���Զ�γ��֣���ĵھ���Ϊ1����
������������ʵʩ�任��ע��1���Զ�γ��֣���ĵھ���Ϊ1����![]() �����п���ȡֵ�ļ���Ϊ_________.
�����п���ȡֵ�ļ���Ϊ_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������P��ABCD�ĵ���Ϊƽ���ı��Σ�PD��ƽ��ABCD��MΪPC�е㣮
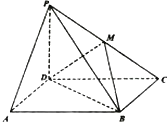
��1����֤��AP��ƽ��MBD��
��2����AD��PB����֤��BD��ƽ��PAD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ���溯����
���溯����
��1����![]() ��
��![]() ��ֵ��
��ֵ��
��2��֤����![]() ������
������![]() �ϵļ�������
�ϵļ�������
��3����![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������BCF��ADE�IJ���CFED��ABFE���DZ߳�Ϊ1�������Σ�M��N����ֱ���AF��CE�ϣ���AM=EN��
��1����֤��ƽ��ABCD��ƽ��ADE��
��2����֤��MN��ƽ��BCF��
��3������NΪEC���е㣬��PΪEF�ϵĶ��㣬����PA+PN����Сֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com