
分析 ①先求出命题p,q成立的等价条件,利用充分而不必要条件的定义,即可得到结论.
②利用向量共线判断P的正误,判断命题q的正误,判断说明真假.
③利用特称命题与全称命题的否定关系判断正误即可.
④利用四种命题的等价关系判断正误即可.
⑤写出逆命题,然后判断真假即可.
⑥利用特例判断充要条件即可.
⑦利用特称命题与全称命题的否定关系判断正误即可.
⑧利用四种命题的逆否关系写出结果即可.
解答 解:对于①,由-4<x-a<4得a-4<x<a+4,
由(x-1)(x-3)<0得1<x<3,
∵q是p的充分而不必要条件,
∴$\left\{\begin{array}{l}a+4≥3\\ a-4≤1\end{array}\right.$,
∴-1≤a≤5,即a的取值范围是[-1,5].所以①正确.
对于②,已知命题p:若$\overrightarrow{a}$=(1,2)与$\overrightarrow{b}$=(-2,λ)共线,可得-4=λ即λ=-4,所以P正确;¬p错误.
命题q:?k∈R,直线y=kx与圆x2+y2-2y=0表示以(0,1)为圆心以1为半径的圆,圆过原点,所以直线y=kx与圆x2+y2-2y=0相交,q是真命题,则¬p∨q是真命题;所以②正确.
对于③,命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R,均有x2+x+1<0”;不满足命题的否定形式,所以③不正确.
对于④,命题“若x=v,则cosx=cosv”是真命题,所以它的逆否命题为真命题;④正确.
对于⑤,命题“若an2<bn2,则a<b”的逆命题是:若a<b,an2<bn2,当n≠0时,an2<bn2.所以⑤不正确.
对于⑥,若x,y∈R,则“x=y”可得xy≥($\frac{x+y}{2}$)2成立,若x,y∈R,xy≥($\frac{x+y}{2}$)2,可得0≥(x-y)2,
可得x=y,所以判断为充要条件;正确.
对于⑦,对命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,则x2+x+1≥0,满足特称命题与全称命题的否定关系,正确.
对于⑧,命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”.满足否命题的形式,正确.
故正确结果为:①②④⑥⑦⑧.
故答案为:①②④⑥⑦⑧.
点评 本题主要考查充分条件和必要条件的应用,命题的否定,四种命题的逆否关系,命题的真假的判断与应用,利用不等式的解法求出不等式的解是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{7}$,$\frac{1}{5}$]∪(5,7] | B. | ($\frac{1}{5}$,$\frac{1}{3}$]∪(5,7] | C. | ($\frac{1}{5}$,$\frac{1}{3}$]∪(3,5] | D. | ($\frac{1}{7}$,$\frac{1}{5}$]∪(3,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x>y | B. | x=y | ||
| C. | x<y | D. | 大小不确定,与m、n的取值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,E为SC的中点,SD=AD.
如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,E为SC的中点,SD=AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
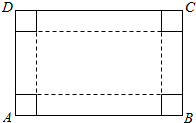 如图,ABCD是长方形硬纸片,AB=80cm,AD=50cm,在硬纸片的四角切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸箱,设切去的小正方形的白边长为x(cm).
如图,ABCD是长方形硬纸片,AB=80cm,AD=50cm,在硬纸片的四角切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸箱,设切去的小正方形的白边长为x(cm).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某市乘坐出租车的收费办法如下:
某市乘坐出租车的收费办法如下:| A. | $y=2[x-\frac{1}{2}]+4$ | B. | $y=2[x-\frac{1}{2}]+5$ | C. | $y=2[x+\frac{1}{2}]+4$ | D. | $y=2[x+\frac{1}{2}]+5$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com