
【题目】如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点. 
(1)求证:平面DFG∥平面ABE;
(2)若AC=2BC=2CD=4,求二面角E﹣AB﹣C的正切值.
【答案】
(1)证明:∵F、G分别是AC、BC中点.
∴FG∥AB,
∵FG平面ABE,AB平面ABE,
∴FG∥平面ABE,
∵DE∥BC,BC=2DE,G是BC中点,
∴DE ![]() BG,∴四边形DEBG是平行四边形,
BG,∴四边形DEBG是平行四边形,
∴DG∥BE,
∵DG平面ABE,BE平面ABE,
∴DG∥平面ABE,
∵DG∩FG=G,DG,FG平面DFG,
AB∩BE=B,AB,BE平面ABE,
∴平面DFG∥平面ABE
(2)解:∵DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.
∴以C为原点,CA为x轴,以CB为y轴,以CD为z轴,建立空间直角坐标系,

∵AC=2BC=2CD=4,
∴A(4,0,0),B(0,2,0),C(0,0,2),E(0,1,2),
![]() =(﹣4,1,2),
=(﹣4,1,2), ![]() =(﹣4,2,0),
=(﹣4,2,0), ![]() =(﹣4,0,2),
=(﹣4,0,2),
设平面ABE的法向量 ![]() =(x,y,z),
=(x,y,z),
则 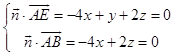 ,取x=1,得
,取x=1,得 ![]() =(1,0,2),
=(1,0,2),
平面ABC的法向量 ![]() =(0,0,1),
=(0,0,1),
则cos< ![]() >=
>= ![]() .
.
∴二面角E﹣AB﹣C的余弦值为cosα= ![]() ,
,
则sinα= ![]() ,tanα=
,tanα= ![]() =
= ![]() .
.
∴二面角E﹣AB﹣C的正切值为 ![]() .
.
【解析】(1)推导出FG∥AB,从而FG∥平面ABE,从而出四边形DEBG是平行四边形,从而DG∥BE,进而DG∥平面ABE,由此能证明平面DFG∥平面ABE.(2)以C为原点,CA为x轴,以CB为y轴,以CD为z轴,建立空间直角坐标系,利用向量法能求出二面角E﹣AB﹣C的正切值.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】某汽车配件厂生产A、B两种型号的产品,A型产品的一等品率为 ![]() ,二等品率为
,二等品率为 ![]() ;B型产品的一等品率为
;B型产品的一等品率为 ![]() ,二等品率为
,二等品率为 ![]() .生产1件A型产品,若是一等品则获得4万元利润,若是二等品则亏损1万元;生产1件B型产品,若是一等品则获得6万元利润,若是二等品则亏损2万元.设生产各件产品相互独立.
.生产1件A型产品,若是一等品则获得4万元利润,若是二等品则亏损1万元;生产1件B型产品,若是一等品则获得6万元利润,若是二等品则亏损2万元.设生产各件产品相互独立.
(1)求生产4件A型产品所获得的利润不少于10万元的概率;
(2)记X(单位:万元)为生产1件A型产品和1件B型产品可获得的利润,求X的分布列及期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点B(﹣1,﹣3),边AB上的高CE所在直线的方程为4x+3y﹣7=0,BC边上中线AD所在的直线方程为x﹣3y﹣3=0.
(1)求点C的坐标;
(2)求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下面材料,尝试类比探究函数y=x2﹣ ![]() 的图象,写出图象特征,并根据你得到的结论,尝试猜测作出函数对应的图象. 阅读材料:
的图象,写出图象特征,并根据你得到的结论,尝试猜测作出函数对应的图象. 阅读材料:
我国著名数学家华罗庚先生曾说:数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休.
在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数的图象的特征.我们来看一个应用函数的特征研究对应图象形状的例子.
对于函数y= ![]() ,我们可以通过表达式来研究它的图象和性质,如:
,我们可以通过表达式来研究它的图象和性质,如: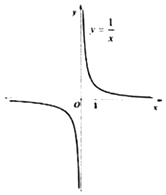
(1)在函数y= ![]() 中,由x≠0,可以推测出,对应的图象不经过y轴,即图象与y轴不相交;由y≠0,可以推测出,对应的图象不经过x轴,即图象与x轴不相交.
中,由x≠0,可以推测出,对应的图象不经过y轴,即图象与y轴不相交;由y≠0,可以推测出,对应的图象不经过x轴,即图象与x轴不相交.
(2)在函数y= ![]() 中,当x>0时y>0;当x<0时y<0,可以推测出,对应的图象只能在第一、三象限;
中,当x>0时y>0;当x<0时y<0,可以推测出,对应的图象只能在第一、三象限;
(3)在函数y= ![]() 中,若x∈(0,+∞)则y>0,且当x逐渐增大时y逐渐减小,可以推测出,对应的图象越向右越靠近x轴;若x∈(﹣∞,0),则y<0,且当x逐渐减小时y逐渐增大,可以推测出,对应的图象越向左越靠近x轴;
中,若x∈(0,+∞)则y>0,且当x逐渐增大时y逐渐减小,可以推测出,对应的图象越向右越靠近x轴;若x∈(﹣∞,0),则y<0,且当x逐渐减小时y逐渐增大,可以推测出,对应的图象越向左越靠近x轴;
(4)由函数y= ![]() 可知f(﹣x)=﹣f(x),即y=
可知f(﹣x)=﹣f(x),即y= ![]() 是奇函数,可以推测出,对应的图象关于原点对称. 结合以上性质,逐步才想出函数y=
是奇函数,可以推测出,对应的图象关于原点对称. 结合以上性质,逐步才想出函数y= ![]() 对应的图象,如图所示,在这样的研究中,我们既用到了从特殊到一般的思想,由用到了分类讨论的思想,既进行了静态(特殊点)的研究,又进行了动态(趋势性)的思考.让我们享受数学研究的过程,传播研究数学的成果.
对应的图象,如图所示,在这样的研究中,我们既用到了从特殊到一般的思想,由用到了分类讨论的思想,既进行了静态(特殊点)的研究,又进行了动态(趋势性)的思考.让我们享受数学研究的过程,传播研究数学的成果.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 过点
过点 ![]() ,离心率为
,离心率为 ![]() ,点F1 , F2分别为其左、右焦点.
,点F1 , F2分别为其左、右焦点.
(1)求椭圆E的标准方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点P,Q,且 ![]() ?若存在,求出该圆的方程,并求|PQ|的最大值;若不存在,请说明理由.
?若存在,求出该圆的方程,并求|PQ|的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆和双曲线焦点F1 , F2相同,且离心率互为倒数,P是椭圆和双曲线在第一象限的交点,当∠F1PF2=60°时,椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com