
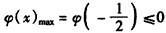 ,
,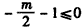 ,
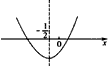
,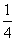 时,f(x)′≤0在[0,1]上恒成立,
时,f(x)′≤0在[0,1]上恒成立,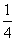 时,
时,
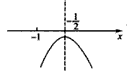
 ,设
,设 ,
,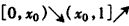 ,
,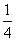 <m<ln2时,f(x)max=f(0)=0;
<m<ln2时,f(x)max=f(0)=0;

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:四川省平武中学2011届高三一诊模拟演练理科数学试题 题型:044
已知二次函数g(x)的图象经过坐标原点,且满足g(x+1)=g(x)+2x+1.设函数f(x)=mg(x)-ln(x+1),其中m为非零常数.
(1)求函数g(x)的解析式;
(2)当-2<m<0时,判断函数f(x)的单调性并且说明理由;
(3)证明:对任意的正整数n,不等式ln(![]() +1)>
+1)>![]() -
-![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源:江苏省无锡市洛社中学2012届高三上学期12月月考数学试题 题型:044
已知二次函数g(x)对任意实数x都满足g(x)=g(1-x),g(x)的最小值为-![]() 且g(1)=-1.令f(x)=g(x+
且g(1)=-1.令f(x)=g(x+![]() )+mlnx+
)+mlnx+![]() (m∈R,x>0).
(m∈R,x>0).
(1)求g(x)的表达式;
(2)若![]() x>0使f(x)≤0成立,求实数m的取值范围;
x>0使f(x)≤0成立,求实数m的取值范围;
(3)设1<m≤e,H(x)=f(x)-(m+1)x,证明:对![]() x1、x2∈[1,m],恒有|H(x1)-H(x2)|<1.
x1、x2∈[1,m],恒有|H(x1)-H(x2)|<1.
查看答案和解析>>
科目:高中数学 来源:山东省模拟题 题型:解答题
 )+mlnx+
)+mlnx+ (m∈R,x>0),
(m∈R,x>0),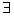 x>0使f(x)≤0成立,求实数m的取值范围;
x>0使f(x)≤0成立,求实数m的取值范围; x1,x2∈[1,m],恒有|H(x1)-H(x2)|<1.
x1,x2∈[1,m],恒有|H(x1)-H(x2)|<1.查看答案和解析>>
科目:高中数学 来源:江苏模拟题 题型:解答题
 )+mlnx+
)+mlnx+ (m∈R),
(m∈R),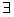 x>0使f(x)≤0成立,求实数m的取值范围;
x>0使f(x)≤0成立,求实数m的取值范围;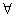 x1,x2∈[1,m],恒有|H(x1)-H(x2)|<1。
x1,x2∈[1,m],恒有|H(x1)-H(x2)|<1。 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com