
【题目】设等差数列![]() 的公差
的公差![]() ,且
,且![]() ,记
,记![]()
(1)用![]() 分别表示
分别表示![]() ,并猜想
,并猜想![]() ;
;
(2)用数学归纳法证明你的猜想.
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为![]() .
.
(1)若出现故障的机器台数为![]() ,求
,求![]() 的分布列;
的分布列;
(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%?
(3)已知一名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润,若该厂现有2名工人,求该厂每月获利的均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
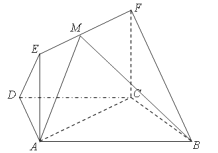
【题目】如图,四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 为梯
为梯
形, ![]() ,
, ![]() ,
, ![]() .且
.且![]() 与
与![]() 均为正三角形,
均为正三角形, ![]() 为
为![]() 的中点,
的中点,
![]() 为
为![]() 重心.
重心.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 的夹角的余弦值.
的夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届广东省深圳市高三下学期第一次调研考试(一模)数学理】已知函数![]() 为自然对数的底数.
为自然对数的底数.
(1)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的值;
的值;
(3)关于![]() 的方程
的方程![]() 有两个实根
有两个实根![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届陕西省西安市铁一中学高三上学期第五次模拟考试数学(理)】已知函数![]() ,其中常数
,其中常数![]() .
.
(Ⅰ)讨论![]() 在
在![]() 上的单调性;
上的单调性;
(Ⅱ)当![]() 时,若曲线
时,若曲线![]() 上总存在相异两点
上总存在相异两点![]() ,使曲线
,使曲线![]() 在
在![]() 两点处的切线互相平行,试求
两点处的切线互相平行,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,空气质量成为人们越来越关注的话题,空气质量指数(![]() ,简称
,简称![]() )是定量描述空气质量状况的指数,空气质量按照
)是定量描述空气质量状况的指数,空气质量按照![]() 大小分为六级,
大小分为六级, ![]() 为优;
为优; ![]() 为良;
为良; ![]() 为轻度污染;
为轻度污染; ![]() 为中度污染;
为中度污染; ![]() 为重度污染;大于300为严重污染.环保部门记录了2017年某月哈尔滨市10天的
为重度污染;大于300为严重污染.环保部门记录了2017年某月哈尔滨市10天的![]() 的茎叶图如下:
的茎叶图如下:

(1)利用该样本估计该地本月空气质量优良(![]() )的天数;(按这个月总共30天计算)
)的天数;(按这个月总共30天计算)
(2)现工作人员从这10天中空气质量为优良的日子里随机抽取2天进行某项研究,求抽取的2天中至少有一天空气质量是优的概率;
(3)将频率视为概率,从本月中随机抽取3天,记空气质量优良的天数为![]() ,求
,求![]() 的概率分布列和数学期望.
的概率分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com