
����Ŀ����֪ij����Ʒÿ�յ�������y����λ�����������ۼ۸�x����λ����Ԫ/�֣�1��x��5�����㣺��1��x��3ʱ��y=a��x��4��2 +![]() ��aΪ����������3��x��5ʱ��y=kx+7��k��0������֪�����ۼ۸�Ϊ3��Ԫ/��ʱ��ÿ�տ��۳�����Ʒ4�֣������ۼ۸�x����3��5]�仯ʱ�����������Ϊ2�֣�
��aΪ����������3��x��5ʱ��y=kx+7��k��0������֪�����ۼ۸�Ϊ3��Ԫ/��ʱ��ÿ�տ��۳�����Ʒ4�֣������ۼ۸�x����3��5]�仯ʱ�����������Ϊ2�֣�
��1����a��k��ֵ����ȷ��y����x�ĺ�������ʽ��
��2��������Ʒ�����۳ɱ�Ϊ1��Ԫ/�֣���ȷ�����ۼ۸�x��ֵ��ʹ��ÿ�����۸���Ʒ�����������
���𰸡���1��![]() ��
�� ��
��
��2��x=2��Ԫ/��ʱ��ÿ�����۸���Ʒ�����������
��������
�����������1��������֪�����ı���ʽ�������������ۼ۸�Ϊ3��Ԫ/��ʱ��ÿ�տ��۳�����Ʒ4�֣������ۼ۸�x����3��5]�仯ʱ�����������Ϊ2�����������![]() ���Ӷ���������ʽ��ע�����ʽ�Ƿֶκ�����
���Ӷ���������ʽ��ע�����ʽ�Ƿֶκ�����
��2������1������������������![]() �ɵ�����1��x��3ʱ������Ϊ
�ɵ�����1��x��3ʱ������Ϊ![]()
![]() �����õ�����֪ʶ����ô�ʱ�����ֵ����3��x��5ʱ��ÿ����������f��x��=����x+7����x��1��=��x2+8x��7���ɶ��κ��������ʿ���ô�ʱ�����ֵ�����߱ȽϿɵ����ֵ��
�����õ�����֪ʶ����ô�ʱ�����ֵ����3��x��5ʱ��ÿ����������f��x��=����x+7����x��1��=��x2+8x��7���ɶ��κ��������ʿ���ô�ʱ�����ֵ�����߱ȽϿɵ����ֵ��
�����������1����Ϊx=3ʱ��y=4������a+3=4����a=1
��3��x��5ʱ��y=kx+7��k��0����������3��5]�����ݼ�����x=5ʱ��ymin=5k+7
��Ϊ���ۼ۸�x����3��5]�仯ʱ�����������Ϊ2�֣�����5k+7=2����k=��1
�� ��
��
��2������1��֪����1��x��3ʱ��
ÿ����������![]() =x3��9x2+24x��10��1��x��3��
=x3��9x2+24x��10��1��x��3��
f'��x��=3x2��18x+24. ��f'��x��=3x2��18x+24��0�����x��4��x��2
����f��x����[1��2]������������[2��3]�����ݼ�
���Ե�x=2��f��x��max=f��2��=10��
��3��x��5ʱ��ÿ����������f��x��=����x+7����x��1��=��x2+8x��7=����x��4��2+9
f��x����x=4ʱ�����ֵ����f��x��max=f��4��=9��f��2��
���ϣ����ۼ۸�x=2��Ԫ/��ʱ��ÿ�����۸���Ʒ�����������


 �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д� С����ȫ�ܼ��ϵ�д�
С����ȫ�ܼ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �У�
�У�![]() �ֱ���
�ֱ���![]() ���е㣬
���е㣬![]() ��������������
��������������![]() .
.
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ��ƽ��ǵ�����ֵ��
��ƽ��ǵ�����ֵ��
��3������![]() ��һ�������Ϊ
��һ�������Ϊ![]() �������ϣ���
�������ϣ���![]() �ı߳�.
�ı߳�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����![]() ʱ������
ʱ������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2��������![]() �����ۺ���
�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��3������2���к���![]() ��������ֵ��
��������ֵ��![]()
![]() ���Ҳ���ʽ
���Ҳ���ʽ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
��
ֱ��![]() ����Բ
����Բ![]() ��һ������Ϊ
��һ������Ϊ![]() ����
����![]() ����Բ
����Բ![]() �ϵ����⡪�㣬�ӳ�
�ϵ����⡪�㣬�ӳ�![]() ����Բ
����Բ![]() �ڵ�
�ڵ�![]() ������
������![]() .
.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����![]() ������Բ������ܳ�.
������Բ������ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������98��Ԫ����һ̨���ػ�����������Ͷ������ʹ�ã��ƻ���һ��ά�ޡ���������12��Ԫ���ӵڶ��꿪ʼ��ÿ������ά�ޡ��������ñ���һ������4��Ԫ���û���ʹ�ú�ÿ���������Ϊ50��Ԫ����ʹ��x������ػ�����ӯ����Ϊy��Ԫ��
(��)д��y��x֮��ĺ�����ϵʽ��
(��)�ӵڼ��꿪ʼ���û�����ʼӯ����ӯ����Ϊ��ֵ����
(��)ʹ��������Ի����Ĵ������������֣�
(1)����ƽ��ӯ����ﵽ���ֵʱ����30��Ԫ�۸����û�����
(2)��ӯ����ﵽ���ֵʱ����12��Ԫ�۸����û�����
�����о�һ�����ַ���������Ϊ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����![]() ��������
��������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2����![]() ����
����![]() ������
������![]()
![]() �ϵ���Сֵ��
�ϵ���Сֵ��
��3��������![]() ��������ֵ��
��������ֵ��![]() ����֤��
����֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
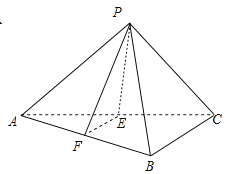
����Ŀ����ͼ����һ���������������P�Dz���ACD�ϵ�һ�㣮
����P��һ������AB��ֱ�Ľ��棬������������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������һ�ַ��������Ч�Ķ�����ʽ������ʦÿ�������������������üƲ�������ͳ�ƣ������8����������������������ͳ��ͼ����Ӧ�������������ݱ����£�


��1��������ʦ��8������������������ƽ������
��2���Ӳ���Ϊ16ǧ����17ǧ����18ǧ����6������ѡ2�죬������ʦ��2��ͨ���������������ĵ�������Ϊ![]() ����
����![]() �ķֲ��м���ѧ������
�ķֲ��м���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.Բ�ĵ�����Բ�棬����������
B.��һ�����ε�ֽƬ���Ծ���һ��Բ
C.һ�������ϡ�������������ȵ�Բ�棬��ô��һ����һ��Բ��
D.Բ̨����������ĸ�ߵ��ӳ��߿����ཻҲ���ܲ��ཻ
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com