
【题目】△ABC的三个内角A、B、C的对边分别是a,b,c,给出下列命题: ①若sinBcosC>﹣cosBsinC,则△ABC一定是钝角三角形;
②若sin2A+sin2B=sin2C,则△ABC一定是直角三角形;
③若bcosA=acosB,则△ABC为等腰三角形;
④在△ABC中,若A>B,则sinA>sinB;
其中正确命题的序号是 . (注:把你认为正确的命题的序号都填上)
【答案】②③④
【解析】解:①若sinBcosC>﹣cosBsinCsinBcosC+cosBsinC=sin(B+C)>00<B+C<π,所以①不一定成立; ②∵sinA= ![]() ,sinB=
,sinB= ![]() ,sinC=
,sinC= ![]() ,∴
,∴ ![]() +
+ ![]() =
= ![]() ,即a2+b2=c2 , ∴△ABC是直角三角形,②成立,
,即a2+b2=c2 , ∴△ABC是直角三角形,②成立,
③若bcosA=acosB2rsinBcosA=2rsinAcosBsin(B﹣A)=0A=B即③成立.
④在△ABC中,若A>Ba>b2rsinA>2rsinBsinA>sinB即④成立;
故正确命题的是②③④.
所以答案是:②③④.
【考点精析】根据题目的已知条件,利用命题的真假判断与应用的相关知识可以得到问题的答案,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


科目:高中数学 来源: 题型:
【题目】如图,江的两岸可近似地看出两条平行的直线,江岸的一侧有![]() ,
, ![]() 两个蔬菜基地,江岸的另一侧点
两个蔬菜基地,江岸的另一侧点![]() 处有一个超市.已知
处有一个超市.已知![]() 、
、![]() 、
、![]() 中任意两点间的距离为
中任意两点间的距离为![]() 千米,超市欲在
千米,超市欲在![]() 之间建一个运输中转站
之间建一个运输中转站![]() ,
, ![]() ,
, ![]() 两处的蔬菜运抵
两处的蔬菜运抵![]() 处后,再统一经过货轮运抵
处后,再统一经过货轮运抵![]() 处,由于
处,由于![]() ,
, ![]() 两处蔬菜的差异,这两处的运输费用也不同.如果从
两处蔬菜的差异,这两处的运输费用也不同.如果从![]() 处出发的运输费为每千米
处出发的运输费为每千米![]() 元.从
元.从![]() 处出发的运输费为每千米
处出发的运输费为每千米![]() 元,货轮的运输费为每千米
元,货轮的运输费为每千米![]() 元.
元.

(1)设![]() ,试将运输总费用
,试将运输总费用![]() (单位:元)表示为
(单位:元)表示为![]() 的函数
的函数![]() ,并写出自变量的取值范围;
,并写出自变量的取值范围;
(2)问中转站![]() 建在何处时,运输总费用
建在何处时,运输总费用![]() 最小?并求出最小值.
最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2≥1}, ![]() ,则A∩(RB)=( )
,则A∩(RB)=( )
A.(2,+∞)
B.(﹣∞,﹣1]∪(2,+∞)
C.(﹣∞,﹣1)∪(2,+∞)
D.[﹣1,0]∪[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对边分别为a,b,c且acosC,bcosB,ccosA成等差数列.
(1)求B的值;
(2)求2sin2A﹣1+cos(A﹣C)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取了40辆汽车在经过路段上某点时的车速(km/h),现将其分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如图所示的频率分布直方图.
,后得到如图所示的频率分布直方图.
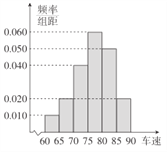
(Ⅰ)现有某汽车途经该点,则其速度低于80km/h的概率约是多少?
(Ⅱ)根据直方图可知,抽取的40辆汽车经过该点的平均速度约是多少?
(Ⅲ)在抽取的40辆且速度在![]() (km/h)内的汽车中任取2辆,求这2辆车车速都在
(km/h)内的汽车中任取2辆,求这2辆车车速都在![]() (km/h)内的概率.
(km/h)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: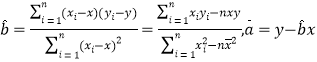 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市某机构为调查2017年下半年落实中学生“阳光体育”活动的情况,设平均每人每天参加体育锻炼时间为![]() (单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
(单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
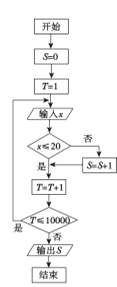
图1
A. 0.64 B. 0.36 C. 6400 D. 3600
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公比为
是公比为![]() 的等比数列,且
的等比数列,且![]() 是
是![]() 与
与![]() 的等比中项,其前
的等比中项,其前![]() 项和为
项和为![]() ;数列
;数列![]() 是等差数列,
是等差数列, ![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() (
(![]() 为常数,且
为常数,且![]() ).
).
(1)求数列![]() 的通项公式及
的通项公式及![]() 的值;
的值;
(2)求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com