
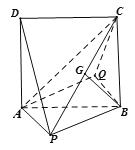
【题目】如图所示的几何体中,正方形![]() 所在平面垂直于平面
所在平面垂直于平面![]() ,四边形
,四边形![]() 为平行四边形,G为
为平行四边形,G为![]() 上一点,且
上一点,且![]() 平面
平面![]() ,
,![]() .
.
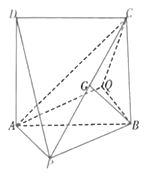
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求平面
体积最大时,求平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(1)证明见解析
(2)![]()
【解析】
(1)利用面面垂直的性质定理可以得到线面垂直,然后得到线线垂直,再由已知的线面垂直得到线线垂直,利用线面垂直的判断定理得到线面垂直,最后利用面面垂直的判定定理证明出面面垂直;
(2)通过三棱锥的体积公式,由等积法可以得到:求三棱锥![]() 体积的最大值,只需求
体积的最大值,只需求![]() 的最大值.设出两个线段的长,建立空间直角坐标系,利用空间向量的数量积公式可以求出平面
的最大值.设出两个线段的长,建立空间直角坐标系,利用空间向量的数量积公式可以求出平面![]() 与平面
与平面![]() 所成二面角的余弦值,最后利用同角的三角函数关系式中的平方和关系求出平面
所成二面角的余弦值,最后利用同角的三角函数关系式中的平方和关系求出平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
(1)证明:因为平面![]()
![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
四边形![]()
![]() 正方形,即
正方形,即![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)解:![]() ,
,
求三棱锥![]() 体积的最大值,只需求
体积的最大值,只需求![]() 的最大值.
的最大值.
令![]() ,
,![]() ,
,
由(1)知,![]() ,
,
所以![]() ,当且仅当
,当且仅当![]() ,
,
即![]() 时,
时,![]() ,
,
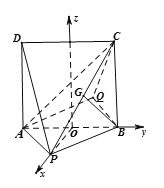
以![]() 中点
中点![]() 为坐标原点建立空间直角坐标系如图,则
为坐标原点建立空间直角坐标系如图,则
![]() ,
,![]() ,
,![]() ,
,![]()
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则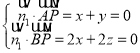 ,
,
可取![]() ,则
,则![]() ,
,
因为四边形![]() 为平行四边形,
为平行四边形,![]() 为等腰直角三角形,
为等腰直角三角形,
所以四边形![]() 为正方形,取平面
为正方形,取平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
即平面![]() 与平面
与平面![]() 所成二面角的正弦值为
所成二面角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】“公平正义”是社会主义和谐社会的重要特征,是社会主义法治理念的价值追求.“考试”作为一种公平公正选拔人才的有效途径,正被广泛采用.每次考试过后,考生最关心的问题是:自己的考试名次是多少?自已能否被录取?能获得什么样的职位?
某单位准备通过考试(按照高分优先录取的原则)录用![]() 名,其中
名,其中![]() 个高薪职位和
个高薪职位和![]() 个普薪职位.实际报名人数为
个普薪职位.实际报名人数为![]() 名,考试满分为
名,考试满分为![]() 分. 考试后对部分考生考试成绩进行抽样分析,得到频率分布直方图如下:
分. 考试后对部分考生考试成绩进行抽样分析,得到频率分布直方图如下:
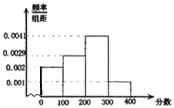
试结合此频率分布直方图估计:
(1)此次考试的中位数是多少分(保留为整数)?
(2)若考生甲的成绩为280分,能否被录取?若能被录取,能否获得高薪职位?(分数精确到个位,概率精确到千分位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业![]() 年的纯利润为
年的纯利润为![]() 万元,因设备老化等原因,企业的生产能力将逐年下降,若不进行技术改造,预测从今年(
万元,因设备老化等原因,企业的生产能力将逐年下降,若不进行技术改造,预测从今年(![]() 年)起每年比上一年纯利润减少
年)起每年比上一年纯利润减少![]() 万元,今年初该企业一次性投入资金
万元,今年初该企业一次性投入资金![]() 万元进行技术改造,预计在未扣除技术改造资金的情况下,第
万元进行技术改造,预计在未扣除技术改造资金的情况下,第![]() 年(今年为第一年)的利润为
年(今年为第一年)的利润为![]() 万元(
万元(![]() 为正整数).
为正整数).
(1)设从今年起的前![]() 年,若该企业不进行技术改造的累计纯利润为
年,若该企业不进行技术改造的累计纯利润为![]() 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为![]() 万元(须扣除技术改造资金),求
万元(须扣除技术改造资金),求![]() ,
,![]() 的表达式;
的表达式;
(2)以上述预测,从今年起该企业至少经过多少年后,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点,x轴的非负半轴为极轴建立极坐标系,并在两种坐标系中取相同的长度单位已知直线l的参数方程为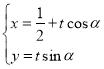 (
(![]() 为参数,
为参数,![]() ),抛物线C的普通方程为
),抛物线C的普通方程为![]() .
.
(1)求抛物线C的准线的极坐标方程;
(2)设直线l与抛物线C相交于A,B两点,求![]() 的最小值及此时
的最小值及此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,已知![]() ,顶点P在平面ABC上的射影为
,顶点P在平面ABC上的射影为![]() 的外接圆圆心.
的外接圆圆心.
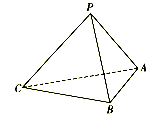
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)若点M在棱PA上,![]() ,且二面角P-BC-M的余弦值为
,且二面角P-BC-M的余弦值为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省新课改后某校为预测2020届高三毕业班的本科上线情况,从该校上一届高三(1)班到高三(5)班随机抽取50人,得到各班抽取的人数和其中本科上线人数,并将抽取数据制成下面的条形统计图.

(1)根据条形统计图,估计本届高三学生本科上线率.
(2)已知该省甲市2020届高考考生人数为4万,假设以(1)中的本科上线率作为甲市每个考生本科上线的概率.
(i)若从甲市随机抽取10名高三学生,求恰有8名学生达到本科线的概率(结果精确到0.01);
(ii)已知该省乙市2020届高考考生人数为3.6万,假设该市每个考生本科上线率均为![]() ,若2020届高考本科上线人数乙市的均值不低于甲市,求p的取值范围.
,若2020届高考本科上线人数乙市的均值不低于甲市,求p的取值范围.
可能用到的参考数据:取![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com