
分析 把数列递推式变形,可得(n+2)•$(\frac{{a}_{n+1}}{{a}_{n}})^{2}+\frac{{a}_{n+1}}{{a}_{n}}=n+1$,即$\frac{{a}_{n+1}}{{a}_{n}}=\frac{n+1}{n+2}$.然后利用累积法得答案.
解答 解:由(n+2)an+12-(n+1)an2+anan+1=0,得
(n+2)•$(\frac{{a}_{n+1}}{{a}_{n}})^{2}+\frac{{a}_{n+1}}{{a}_{n}}=n+1$,即
$\frac{{a}_{n+1}}{{a}_{n}}=\frac{n+1}{n+2}$.
∴${a}_{n}=\frac{{a}_{n}}{{a}_{n-1}}•\frac{{a}_{n-1}}{{a}_{n-2}}•…•\frac{{a}_{2}}{{a}_{1}}•{a}_{1}$
=$\frac{n}{n+1}•\frac{n-1}{n}•…•\frac{2}{3}•1=\frac{2}{n+1}$.
故答案为:$\frac{2}{n+1}$.
点评 本题考查数列递推式,考查了累积法求数列的通项公式,是中档题.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32}{3}$π | B. | $\frac{16}{3}$π | C. | 32π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=sin2x+cos2x | B. | f(x)=sin2x | C. | f(x)=tan(x+$\frac{π}{8}$) | D. | f(x)=cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
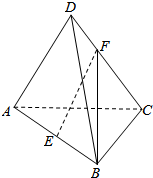 如图,在空间四边形ABCD中,E是线段AB的中点.
如图,在空间四边形ABCD中,E是线段AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{OC}$=sinα$\overrightarrow{OA}$+cosα$\overrightarrow{OB}$ | B. | $\overrightarrow{OC}$=sin2α$\overrightarrow{OA}$+cos2α$\overrightarrow{OB}$ | ||
| C. | $\overrightarrow{OC}$=sinα$\overrightarrow{OA}$-cosα$\overrightarrow{OB}$ | D. | $\overline{OC}$=sin2α$\overrightarrow{OA}$-cos2α$\overrightarrow{OB}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com