
(本小题满分14分)如图,长方体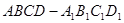 中,
中, ,
,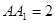 ,
,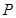 为
为 的中点。
的中点。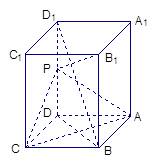
(1)求证:直线 ∥平面
∥平面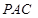 ;
;
(2)求证:平面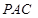
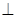 平面
平面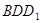 ;
;
(3)求证:直线
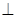 平面
平面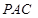 。
。
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
(14分)如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为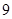 m,
m,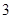 m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕
m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕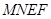 ,
,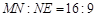 .线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).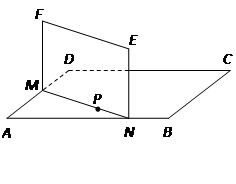
(1)求S关于x的函数关系式及该函数的定义域;
(2)当x取何值时,液晶广告屏幕MNEF的面积S最小?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)如图,有三个生活小区(均可看成点)分别位于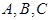 三点处,
三点处,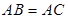 ,
,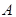 到线段
到线段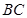 的距离
的距离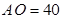 ,
,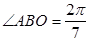 (参考数据:
(参考数据: 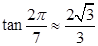 ). 今计划建一个生活垃圾中转站
). 今计划建一个生活垃圾中转站 ,为方便运输,
,为方便运输, 准备建在线段
准备建在线段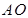 (不含端点)上.
(不含端点)上.
(1)设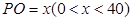 ,试将
,试将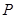 到三个小区距离的最远者
到三个小区距离的最远者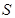 表示为
表示为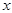 的函数,并求
的函数,并求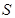 的最小值;
的最小值;
(2)设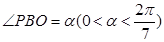 ,试将
,试将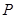 到三个小区的距离之和
到三个小区的距离之和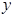 表示为
表示为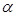 的函数,并确定当
的函数,并确定当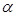 取何值时,可使
取何值时,可使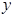 最小?
最小?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分10分) 在长方体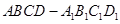 中,
中,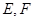 分别是
分别是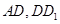 的中点,
的中点,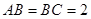 ,
,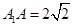 .
.
(Ⅰ)求证: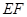 //平面
//平面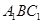 ;
;
(Ⅱ)在线段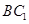 上是否存在点
上是否存在点 ,使直线
,使直线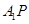 与
与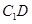 垂直,
垂直,
如果存在,求线段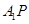 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.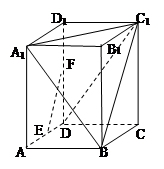
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)如图(甲),在直角梯形ABED中,AB//DE,AB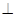 BE,AB
BE,AB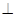 CD,且BC=CD,AB=2,F、H、G分别为AC ,AD ,DE的中点,现将△ACD沿CD折起,使平面ACD
CD,且BC=CD,AB=2,F、H、G分别为AC ,AD ,DE的中点,现将△ACD沿CD折起,使平面ACD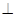 平面CBED,如图(乙).
平面CBED,如图(乙).
(1)求证:平面FHG//平面ABE;
(2)记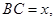
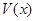 表示三棱锥B-ACE 的体积,求
表示三棱锥B-ACE 的体积,求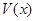 的最大值;
的最大值;
(3)当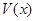 取得最大值时,求二面角D-AB-C的余弦值.
取得最大值时,求二面角D-AB-C的余弦值.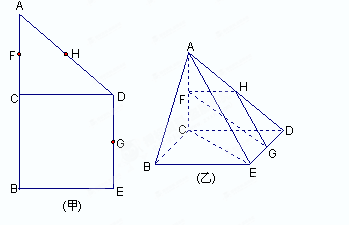
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com