
| 年份 x | 1950 | 1951 | 1952 | 1953 | 1954 | 1955 | 1956 | 1957 | 1958 |
| 人数 Y/万人 | 55 196 | 56 300 | 57 482 | 58 796 | 60 266 | 61 560 | 62 828 | 64 563 | 65 994 |
分析 利用变换的方法,结合线性回归方程,求 y 关于 x 的非线性回归方程.
解答 解:根据收集数据,作散点图.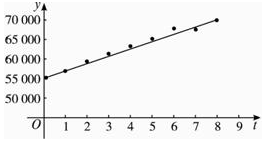
根据已有函数知识,发现样本点分布在某一条指数函数周围,y=c 1e c2x(其中 c 1,c 2是待定参数).
令 z=ln y,则有 y=e z,
∴e z=e lnc1+c 2x.
z=c 2x+ln c 1=bx+a,
变换后:
| x | 1950 | 1951 | 1952 | 1953 | 1954 | 1955 | 1956 | 1957 | 1958 |
| z=ln y | 10.92 | 10.94 | 10.96 | 10.98 | 11.01 | 11.03 | 11.05 | 11.08 | 11.09 |
点评 本题考查回归方程,考查换元方法的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (0,2) | C. | (0,2)∪(-∞,-1) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{{n^2}-n}}{2}$ | B. | $\frac{n^2}{2}$ | C. | $\frac{{{n^2}+n}}{2}$ | D. | $\frac{{{n^2}+2n}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{4}{5}$,-$\frac{2}{5}$) | B. | (-$\frac{2}{5}$,$\frac{4}{5}$) | C. | ($\frac{4}{5}$,$\frac{2}{5}$) | D. | ($\frac{2}{5}$,-$\frac{4}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
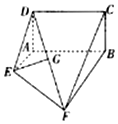 已知多面体ABCDEF如图所示,其中ABCD为矩形,△DAE为等腰等腰三角形,DA⊥AE,四边形AEFB为梯形,且AE∥BF,∠ABF=90°,AB=BF=2AE=2.
已知多面体ABCDEF如图所示,其中ABCD为矩形,△DAE为等腰等腰三角形,DA⊥AE,四边形AEFB为梯形,且AE∥BF,∠ABF=90°,AB=BF=2AE=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com