
【题目】如图,已知三棱柱![]() 的侧棱垂直于底面,
的侧棱垂直于底面,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 和
和![]() 的中点.
的中点.

(1)若![]() ,求三棱柱
,求三棱柱![]() 的体积;
的体积;
(2)证明:![]() 平面
平面![]() ;
;
(3)请问当![]() 为何值时,
为何值时,![]() 平面
平面![]() ,试证明你的结论.
,试证明你的结论.
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
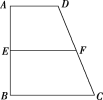
【题目】如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,将四边形
的中点,将四边形![]() 沿直线
沿直线![]() 进行翻折,给出下列四个结论:①
进行翻折,给出下列四个结论:①![]() ;②
;②![]() ③平面
③平面![]() 平面
平面![]() ;④平面
;④平面![]() 平面
平面![]() ,则上述结论可能正确的是( ).
,则上述结论可能正确的是( ).
A.①③B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
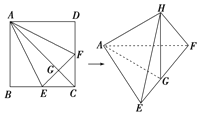
【题目】如图,在正方形ABCD中,E、F分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个空间图形,使B、C、D三点重合,重合后的点记为H,那么,在这个空间图形中必有( )
A. ![]() 所在平面B.
所在平面B. ![]() 所在平面
所在平面
C. ![]() 所在平面D.
所在平面D. ![]() 所在平面
所在平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象经过(-1,0)点,且在x=-1处的切线斜率为-1,设数列
的图象经过(-1,0)点,且在x=-1处的切线斜率为-1,设数列![]() 的前n项和Sn=f(n)(n∈N*).
的前n项和Sn=f(n)(n∈N*).
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列{![]() }前n项的和Tn.
}前n项的和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位为了响应疫情期间有序复工复产的号召,组织从疫区回来的甲、乙、丙、丁4名员工进行核酸检测,现采用抽签法决定检测顺序,在“员工甲不是第一个检测,员工乙不是最后一个检测”的条件下,员工丙第一个检测的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定空间中十个点,其中任意四点不在一个平面上,将某些点之间用线段相连,若得到的图形中没有三角形也没有空间四边形,试确定所连线段数目的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com