
【题目】平行六面体![]() 中,以顶点
中,以顶点![]() 为端点的三条棱长都为1,且两两夹角为
为端点的三条棱长都为1,且两两夹角为![]() .
.

(1)求![]() 的长;
的长;
(2)求异面直线![]() 与
与![]() 夹角的余弦值.
夹角的余弦值.
【答案】(1)AC1的长为![]() ;(2)AC与BD1夹角的余弦值为
;(2)AC与BD1夹角的余弦值为![]() 。
。
【解析】
试题(1)记![]() =a,
=a,![]() =b,
=b,![]() =c,并将其作为一组基底,利用空间向量的基本定理表示出
=c,并将其作为一组基底,利用空间向量的基本定理表示出![]() ,然后利用向量的模长计算公式及数量积的运算律即可求解;(2)利用向量夹角求两条异面直线夹角,但注意向量夹角为锐角或直角时两者相等,当向量夹角为钝角时,两者互补。
,然后利用向量的模长计算公式及数量积的运算律即可求解;(2)利用向量夹角求两条异面直线夹角,但注意向量夹角为锐角或直角时两者相等,当向量夹角为钝角时,两者互补。
试题解析:(1)记![]() =a,
=a,![]() =b,
=b,![]() =c,
=c,
则|a|=|b|=|c|=1,〈a,b〉=〈b,c〉=〈c,a〉=60°,
∴a·b=b·c=c·a=![]() .
.
|![]() |2=(a+b+c)2=a2+b2+c2+2(a·b+b·c+c·a)=1+1+1+2×
|2=(a+b+c)2=a2+b2+c2+2(a·b+b·c+c·a)=1+1+1+2×![]() =6,
=6,
∴|![]() |=
|=![]() ,即AC1的长为
,即AC1的长为![]() .
.
(2)![]() =b+c-a,
=b+c-a,![]() =a+b,∴|
=a+b,∴|![]() |=
|=![]() ,|
,|![]() |=
|=![]() ,
,
![]() ·
·![]() =(b+c-a)·(a+b)=b2-a2+a·c+b·c=1.
=(b+c-a)·(a+b)=b2-a2+a·c+b·c=1.
∴cos〈![]() ,
,![]() 〉=
〉=![]() =
=![]() .
.
∴AC与BD1夹角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() 的焦点为F,抛物线C与直线l1:
的焦点为F,抛物线C与直线l1:![]() 的一个交点为
的一个交点为![]() ,且
,且![]() (
(![]() 为坐标原点).
为坐标原点).
(Ⅰ)求抛物线C的方程;
(II)不过原点的直线l2与l1垂直,且与抛物线交于不同的两点A,B,若线段AB的中点为P,且|OP|=|PB|,求△FAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网约车的兴起丰富了民众出行的选择,为民众出行提供便利的同时也解决了很多劳动力的就业问题,据某著名网约车公司“滴滴打车”官网显示,截止目前,该公司已经累计解决退伍军人转业为兼职或专职司机三百多万人次,梁某即为此类网约车司机,据梁某自己统计某一天出车一次的总路程数可能的取值是20、22、24、26、28、![]() ,它们出现的概率依次是
,它们出现的概率依次是![]() 、
、![]() 、
、![]() 、
、![]() 、t、
、t、![]() .
.
(1)求这一天中梁某一次行驶路程X的分布列,并求X的均值和方差;
(2)网约车计费细则如下:起步价为5元,行驶路程不超过![]() 时,租车费为5元,若行驶路程超过
时,租车费为5元,若行驶路程超过![]() ,则按每超出
,则按每超出![]() (不足
(不足![]() 也按
也按![]() 计程)收费3元计费.依据以上条件,计算梁某一天中出车一次收入的均值和方差.
计程)收费3元计费.依据以上条件,计算梁某一天中出车一次收入的均值和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力,某移动支付公司在我市随机抽取了100名移动支付用户进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)在每周使用移动支付超过3次的样本中,按性别用分层抽样的方法随机抽取5名用户.
①求抽取的5名用户中男、女用户各多少人;
②从这5名用户中随机抽取2名用户,求抽取的2名用户中既有男用户又有女用户的概率.
(2)如果认为每周使用移动支付次数超过3次的用户“喜欢使用移动支付”,能否在犯错误概率不超过![]() 的前提下,认为“喜欢使用移动支付”与性别有关?
的前提下,认为“喜欢使用移动支付”与性别有关?
附表及公式:
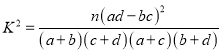
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海岸![]() 处,发现北偏东
处,发现北偏东![]() 方向,距离
方向,距离![]() 为
为![]() 海里的
海里的![]() 处有一艘走私船,在
处有一艘走私船,在![]() 处北偏西
处北偏西![]() 方向,距离
方向,距离![]() 为
为![]() 海里的
海里的![]() 处有一艘缉私艇奉命以
处有一艘缉私艇奉命以![]() 海里/时的速度追截走私船,此时,走私船正以
海里/时的速度追截走私船,此时,走私船正以![]() 海里/时的速度从
海里/时的速度从![]() 处向北偏东
处向北偏东![]() 方向逃窜.
方向逃窜.
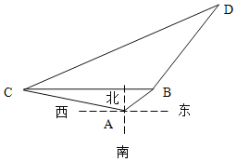
(1)问![]() 船与
船与![]() 船相距多少海里?
船相距多少海里?![]() 船在
船在![]() 船的什么方向?
船的什么方向?
(2)问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() 和
和![]() 均为等边三角形,且平面
均为等边三角形,且平面![]() 平面
平面![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
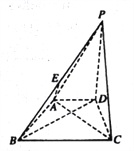
(1)求证: ![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com