
分析 设出过焦点的直线方程,与双曲线的渐近线方程联立把A,B表示出来,再由条件可得A为F1B的中点,运用中点坐标公式,可得a,b,c的关系,然后求双曲线的离心率.
解答 解:设F1(-c,0),则过F1作斜率为1的直线为:y=x+c,
而渐近线的方程是:y=±$\frac{b}{a}$x,
由$\left\{\begin{array}{l}{y=x+c}\\{y=-\frac{b}{a}x}\end{array}\right.$得:A(-$\frac{ac}{a+b}$,$\frac{bc}{a+b}$),
由$\left\{\begin{array}{l}{y=x+c}\\{y=\frac{b}{a}x}\end{array}\right.$得,B(-$\frac{ac}{a-b}$,-$\frac{bc}{a-b}$),
若$\frac{|A{F}_{1}|}{|B{F}_{1}|}$=$\frac{1}{2}$,可得A为F1B的中点,
可得-c-$\frac{ac}{a-b}$=-2•$\frac{ac}{a+b}$,
化为b=3a,c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{10}$a,
∴e=$\frac{c}{a}$=$\sqrt{10}$.
故答案为$\sqrt{10}$.
点评 本题考查双曲线的性质和应用,主要是离心率的求法,解题时要认真审题,仔细解答,注意中点坐标公式的合理运用.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 可能有两支队伍得分都是18分 | B. | 各支队伍得分总和为180分 | ||
| C. | 各支队伍中最高得分不少于10分 | D. | 得偶数分的队伍必有偶数个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
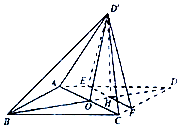 如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=EF,EF交BD于点H,将△DEF沿EF折到△D'EF的位置.
如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=EF,EF交BD于点H,将△DEF沿EF折到△D'EF的位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com