
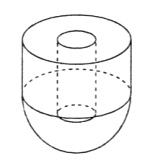
【题目】如图所示,某几何体由底面半径和高均为5的圆柱与半径为5的半球面对接而成,该封闭几何体内部放入一个小圆柱体,且圆柱体的上下底面均与外层圆柱的底面平行,则小圆柱体积的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】圆周上有1994个点,将它们染成若干种不同的颜色,且每种颜色的点数各不相同.今在每种颜色的点集中各取一个点,组成顶点颜色各不相同的圆内接多边形,为了要使这样的多边形个数最多,应将1994个点染成多少种不同的颜色?且每种颜色的点集各含有多少个点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年某地遭遇严重干旱,某乡计划向上级申请支援,为上报需水量,乡长事先抽样调查100户村民的月均用水量,得到这100户村民月均用水量(单位:t)的频率分布表如下:
月均用水量分组 | 频数 | 频率 |
| 12 | |
| ||
| 40 | |
| 0.18 | |
| 6 | |
合计 | 100 | 1.00 |
(1)请完成该频率分布表,并画出相对应的频率分布直方图.
(2)样本的中位数是多少?
(3)已知上级将按每户月均用水量向该乡调水,若该乡共有1200户,请估计上级支援该乡的月调水量是多少吨.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点M到定点F1(-2,0)和F2(2,0)的距离之和为![]() .
.
(1)求动点M轨迹C的方程;
(2)设N(0,2),过点P(-1,-2)作直线l,交椭圆C于不同于N的A,B两点,直线NA,NB的斜率分别为k1,k2,问k1+k2是否为定值?若是的求出这个值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】统计表明,某种型号的汽车在匀速行驶中每小时耗油量![]() (升)关于行驶速度
(升)关于行驶速度![]() (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: ![]() ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ,若g(x)=f(x)-a恰好有3个零点,则a的取值范围为( )
,若g(x)=f(x)-a恰好有3个零点,则a的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
![]() 恰好有3个零点, 等价于
恰好有3个零点, 等价于![]() 的图象有三个不同的交点,
的图象有三个不同的交点,
作出![]() 的图象,根据数形结合可得结果.
的图象,根据数形结合可得结果.

![]() 恰好有3个零点,
恰好有3个零点,
等价于![]() 有三个根,
有三个根,
等价于![]() 的图象有三个不同的交点,
的图象有三个不同的交点,
作出![]() 的图象,如图,
的图象,如图,
由图可知,
当![]() 时,
时,![]() 的图象有三个交点,
的图象有三个交点,
即当![]() 时,
时,![]() 恰好有3个零点,
恰好有3个零点,
所以,![]() 的取值范围是
的取值范围是![]() ,故选D.
,故选D.
【点睛】
本题主要考查函数的零点与分段函数的性质,属于难题. 函数的性质问题以及函数零点问题是高考的高频考点,考生需要对初高中阶段学习的十几种初等函数的单调性、奇偶性、周期性以及对称性非常熟悉;另外,函数零点的几种等价形式:函数![]() 的零点
的零点![]() 函数
函数![]() 在
在![]() 轴的交点
轴的交点![]() 方程
方程![]() 的根
的根![]() 函数
函数![]() 与
与![]() 的交点.
的交点.
【题型】单选题
【结束】
13
【题目】设集合A={0,log3(a+1)},B={a,a+b}若A∩B={1},则b=______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 的焦点,若点
的焦点,若点![]() 在抛物线
在抛物线![]() 上,且
上,且![]()
![]() 求抛物线
求抛物线![]() 的方程;
的方程;
![]() 动直线
动直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,问:在
两点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() 其中
其中![]() ,使得向量
,使得向量![]() 与向量
与向量![]() 共线
共线![]() 其中
其中![]() 为坐标原点
为坐标原点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(Ⅰ)将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为三次函数,且其图象关于原点对称,当
为三次函数,且其图象关于原点对称,当![]() 时,
时,![]() 的极小值为-1,则
的极小值为-1,则
(1)函数的解析式![]() __________;
__________;
(2)函数![]() 的单调递增区间为___________。
的单调递增区间为___________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com