
【题目】已知函数![]() .
.
(1)若![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线在两坐标轴上的截距之和为
处的切线在两坐标轴上的截距之和为![]() ,求
,求![]() 的值;
的值;
(2)若对于任意的![]() 及任意的
及任意的![]() ,总有
,总有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】(2016·威海模拟)三人参加某娱乐闯关节目,假设甲闯关成功的概率是![]() ,乙、丙两人同时闯关成功的概率是
,乙、丙两人同时闯关成功的概率是![]() ,甲、丙两人同时闯关失败的概率是
,甲、丙两人同时闯关失败的概率是![]() ,且三人各自能否闯关成功相互独立.
,且三人各自能否闯关成功相互独立.
(1)求乙、丙两人各自闯关成功的概率;
(2)设ξ表示三人中最终闯关成功的人数,求ξ的分布列和均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型高端制造公司为响应《中国制造2025》中提出的坚持“创新驱动、质量为先、绿色发展、结构优化、人才为本”的基本方针,准备加大产品研发投资,下表是该公司2017年5~12月份研发费用(百万元)和产品销量(万台)的具体数据:

(1)根据数据可知![]() 与
与![]() 之间存在线性相关关系
之间存在线性相关关系
(i)求出![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(ii)若2018年6月份研发投人为25百万元,根据所求的线性回归方程估计当月产品的销量;
(2)为庆祝该公司9月份成立30周年,特制定以下奖励制度:以![]() (单位:万台)表示日销量,
(单位:万台)表示日销量, ![]() ,则每位员工每日奖励
,则每位员工每日奖励![]() 元;
元;![]() ,则每位员工每日奖励
,则每位员工每日奖励![]() 元;
元;![]() ,则每位员工每日奖励
,则每位员工每日奖励![]() 元现已知该公司9月份日销量
元现已知该公司9月份日销量![]() (万台)服从正态分布
(万台)服从正态分布![]() ,请你计算每位员工当月(按
,请你计算每位员工当月(按![]() 天计算)获得奖励金额总数大约多少元.
天计算)获得奖励金额总数大约多少元.
参考数据: ![]() ,
,![]() .
.
参考公式:对于一组数据![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:  ,
,![]() .
.
若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]()
![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:![]() (a>0),过点P(-2,-4)的直线l的参数方程为
(a>0),过点P(-2,-4)的直线l的参数方程为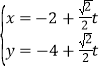 (t为参数),l与C分别交于M,N.
(t为参数),l与C分别交于M,N.
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,
,![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调区间;
的单调区间;
(3)如果![]() 、
、![]() 、
、![]() 满足
满足![]() ,那么称
,那么称![]() 比
比![]() 更靠近
更靠近![]() .当
.当![]() 且
且![]() 时,试比较
时,试比较![]() 和
和![]() 哪个更靠近
哪个更靠近![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知倾斜角为
中,已知倾斜角为![]() 的直线
的直线![]() 经过点
经过点![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)写出曲线![]() 的普通方程;
的普通方程;
(2)若直线![]() 与曲线
与曲线![]() 有两个不同的交点
有两个不同的交点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加数学与地理的学业水平测试,从中随机抽取100人的数学与地理的学业水平测试成绩如下表:
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
地理 | 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 | a | 4 | b | |
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩例如:表示数学成绩为良好的共有20+18+4=42(人).
(Ⅰ)若在该样本中,数学成绩优秀率为30%,求a,b的值;
(Ⅱ)已知a≥10,b≥8,利用样本数据,求数学成绩为优秀的人数比及格的人数少的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com