
 是平面内不共线的向量,
是平面内不共线的向量, 是平面内任一向量,关于实数x的方程
是平面内任一向量,关于实数x的方程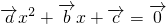 ,下列说法正确的是
,下列说法正确的是 x2+
x2+ x+
x+ =
= ,可转化为
,可转化为 =-x2
=-x2 -x
-x ,由向量
,由向量 、
、 不共线,根据平面向量的基本定理我们易判断存在有且仅有一对实数λ1、λ2,满足方程,即λ1=-x2且λ2=-x,根据实数
不共线,根据平面向量的基本定理我们易判断存在有且仅有一对实数λ1、λ2,满足方程,即λ1=-x2且λ2=-x,根据实数 =-x2
=-x2 -x
-x ,∵
,∵ 、
、 不共线,可视为“基底”,
不共线,可视为“基底”,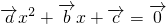 至多有一个解,
至多有一个解,

 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
①两两相交的三条直线只可能确定一个平面;
②经过平面外一点,有且仅有一个平面垂直这个平面;
③平面α内不共线的三点到平面β的距离相等,则α∥β;
④两个平面垂直,过其中一个平面内一点作它们交线的垂线,则此垂线垂直于另一个平面
其中真命题的个数是( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| A.有两个不同的解 | B.只有一解 |
| C.至多有一个解 | D.无解 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com