
【题目】选修4-4:极坐标与参数方程
已知在平面直角坐标系xOy中,O为坐标原点,曲线C:  (α为参数),在以平面直角坐标系的原点为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系,直线l:ρ
(α为参数),在以平面直角坐标系的原点为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系,直线l:ρ![]() .
.
(Ⅰ)求曲线C的普通方程和直线l的直角坐标方程;
(Ⅱ)曲线C上恰好存在三个不同的点到直线l的距离相等,分别求出这三个点的极坐标.
【答案】(Ⅰ)见解析;(Ⅱ)见解析.
【解析】试题分析: (1)消去参数α,即可得到曲线C的普通方程,利用极坐标与直角坐标互化求出直线l的直角坐标方程;
(2)求出圆的圆心与半径,求出三个点的坐标,然后求解极坐标.
试题解析:
(Ⅰ)曲线![]() ,
,
可得:![]()
曲线C的普通方程:x2+y2=4.
直线l:ρsin![]() =1=
=1=![]() ρsin θ+
ρsin θ+![]() ρcos θ,
ρcos θ,
直线l的直角坐标方程:x+![]() y-2=0.
y-2=0.
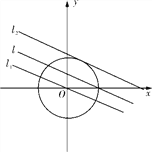
(Ⅱ)∵圆C的圆心(0,0)半径为2,,圆心C到直线的距离为1,
∴这三个点在平行直线l1与 l2上,如图:直线l1与 l2与l的距离为1.
l1:x+![]() y=0,l2:x+
y=0,l2:x+![]() y-4=0.
y-4=0.
![]() ,可得
,可得![]()
![]()
两个交点(-![]() ,1)、(
,1)、(![]() ,-1);
,-1);
![]()
解得(1,![]() ),
),
这三个点的极坐标分别为:![]() 、
、![]() 、
、![]() .
.


科目:高中数学 来源: 题型:
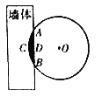
【题目】《九章算术》是我国古代数学经典名著,其中有这样一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有-圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该木材,锯口深一寸,锯道长-尺.问这块圆柱形木材的直径是多少?现有长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌在墙体中的体积约为__________立方寸.(结果保留整数)
寸,估算该木材镶嵌在墙体中的体积约为__________立方寸.(结果保留整数)
注:l丈=10尺=100寸,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 为其前
为其前![]() 项的和,满足
项的和,满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:当
,求证:当![]() 时
时![]() ;
;
(3)(理)已知当![]() ,且
,且![]() 时有
时有![]() ,其中
,其中![]() ,求满足
,求满足![]() 的所有
的所有![]() 的值.
的值.
(4)(文)若函数![]() 的定义域为
的定义域为![]() ,并且
,并且![]() ,求证
,求证![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知顶点为原点的抛物线C的焦点与椭圆![]() 的上焦点重合,且过点
的上焦点重合,且过点![]() .
.
(1)求椭圆的标准方程;
(2)若抛物线上不同两点A,B作抛物线的切线,两切线的斜率![]() ,若记AB的中点的横坐标为m,AB的弦长
,若记AB的中点的横坐标为m,AB的弦长![]() ,并求
,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知箱中装有10个不同的小球,其中2个红球、3个黑球和5个白球,现从该箱中有放回地依次取出3个小球.则3个小球颜色互不相同的概率是______;若变量![]() 为取出3个球中红球的个数,则
为取出3个球中红球的个数,则![]() 的方差
的方差![]() ______.
______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com