
����Ŀ��С��ÿ��ӼҲ���ȥѧУ��������·�߿���ѡ��һ��·�ߣ��������ţ����õȺ�ƣ�ƽ����ʱ910�룻�ڶ���·�ߣ�Ҫ�����������̵�·�ڣ���ͼ��A��ΪС���ң�D��ΪѧУ����·��![]() ��240�룬��B����һ���̵ƣ����ʱ��120�룬�̵�ʱ��30�룬��·��
��240�룬��B����һ���̵ƣ����ʱ��120�룬�̵�ʱ��30�룬��·��![]() ��450�룬��C��Ҳ��һ���̵ƣ����ʱ��100�룬�̵�ʱ��50�룬��·��
��450�룬��C��Ҳ��һ���̵ƣ����ʱ��100�룬�̵�ʱ��50�룬��·��![]() ��200��.С��������60������飬ÿ�춼ѡ��ڶ���·�ߣ�����¼����B���ȴ���Ƶ�ʱ������ͳ�ƣ�60������48����B��������ƣ����ݼ�¼��48��ȴ����ʱ�������ݻ����������Ƶ�ʷֲ�ֱ��ͼ.��֪B����C���ĺ�������ʱ��ǡ��ʼ�ձ�����ͬ���Һ��̵�֮���л���ʱ����.
��200��.С��������60������飬ÿ�춼ѡ��ڶ���·�ߣ�����¼����B���ȴ���Ƶ�ʱ������ͳ�ƣ�60������48����B��������ƣ����ݼ�¼��48��ȴ����ʱ�������ݻ����������Ƶ�ʷֲ�ֱ��ͼ.��֪B����C���ĺ�������ʱ��ǡ��ʼ�ձ�����ͬ���Һ��̵�֮���л���ʱ����.

��1����С��ѡ��ڶ���·�ߣ��赱С������B����ʱ��ΪB����������ĵ�x�루![]() ��ʱ��С����B���ȴ���Ƶ�ʱ��Ϊy�룬��y����x�ĺ����Ľ���ʽ��
��ʱ��С����B���ȴ���Ƶ�ʱ��Ϊy�룬��y����x�ĺ����Ľ���ʽ��
��2����С��ѡ��ڶ���·�ߣ������С����B��������Ƶĸ��ʣ�����С���Ƿ������B����C����������ƣ�
��3����ȡ�����е���Ϊ�������Ӧ�ĵȴ���Ƶ�ʱ������������·�ߵ�ƽ����ʱ��Ϊ�������ݣ�С��Ӧѡ����һ��·�ߣ�
���𰸡���1��![]() ����2������С����
����2������С����![]() ��������Ƶĸ���Ϊ
��������Ƶĸ���Ϊ![]() ��С����������
������������![]() ����
����![]() ����������ƣ���3��С��Ӧ��ѡ���һ��·��.
����������ƣ���3��С��Ӧ��ѡ���һ��·��.
��������
��1���ֱ���![]() ��
��![]() ��������µõ��ȴ����ʱ���������õ������
��������µõ��ȴ����ʱ���������õ������
��2�����ݼ��θ����ʹ�ʽ����ɵ�������ʣ������������̵Ƶ���ʱ����Ϊ![]() ��ʱ����
��ʱ����![]() �����жϳ�����ͬʱ������ƣ�
�����жϳ�����ͬʱ������ƣ�
��3������Ƶ�ʷֲ�ֱ��ͼ����ɵõȴ���Ƶ�ƽ��ʱ��������ȷ���ڶ���·�ߵ�ƽ��ʱ�����Ӷ�ȷ�����.
��1����![]() ʱ��С���ȴ����ʱ��
ʱ��С���ȴ����ʱ��![]() ��
��
��![]() ʱ��С������ȴ�����
ʱ��С������ȴ�����![]() ��
��
����������![]() .
.
��2������С����![]() ��������Ƶĸ���
��������Ƶĸ���![]() .
.
��ΪС����![]() ����ʱ��һ����
����ʱ��һ����![]() ���������
���������![]() ���
���![]() ��
��![]() ���ĺ�������ʱ��ǡ��ʼ�ձ�����ͬ����
���ĺ�������ʱ��ǡ��ʼ�ձ�����ͬ����![]() ����
����![]() �����̵Ƶ�ʱ������ȣ�������С����·��
�����̵Ƶ�ʱ������ȣ�������С����·��![]() �����ʱ��
�����ʱ��![]() ���
���![]() ������������
������С������![]() ����ʱ��һ����
����ʱ��һ����![]() ���������
���������![]() ��֮������С��������
��֮������С��������![]() ��������ƣ����С����������
��������ƣ����С����������![]() ����
����![]() �����������.
�����������.
��3��С���ߵڶ���·��ƽ���ȴ���Ƶ�ʱ��Ϊ��
![]()
![]() ���룩��
���룩��
С���ߵڶ���·��ƽ����ʱΪ��![]() ���룩��
���룩��
![]() ��
��![]() С��Ӧ��ѡ���һ��·��.
С��Ӧ��ѡ���һ��·��.


 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ����Ⱥ�ڲ�����ȫ������������Ӳ�������Ȥζ��.���췽�������һ��С��Ϸ������������һö�ʵؾ��ȵ����ӣ������壬�������Ϸֱ��ע1��2��3��4��5��6�������֣�.�����ϵĵ���Ϊż��.���������һ��.�����ϵĵ���Ϊ��������ֹͣ��Ϸ���������Ĺ�����У������������3��.ÿλ������ֻ�ܲμ�һ����Ϸ.
��1������Ϸ����ʱ���ϵ���֮��Ϊ5�ĸ��ʣ�
��2�������߿���ѡ�����ַ���������һ����Ϸ����ʱ�������ϵĵ���֮��Ϊż��������3����ͬ�ij����飻�����ϵĵ���֮��Ϊ����������1��������.����������Ϸ����ʱ�����һ�γ��ϵĵ���Ϊż��������5����ͬ�ij����飬��������.�Է�����һ�ַ�����ʹ��Ϸ������ø��೩���齱������˵���жϵ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г���·���ߴ������㳡Ҫ���һ����������ͼ1���������ܸ߶�Ϊ12�ף���������������ɣ��ϰ벿�����ĸ���ֱ��ˮƽ����ĵȸߴ�ֱ������ɣ��������ֺ��Բ��ƣ����°벿����������̨���ϵ����ĸ�ˮƽ������������̨���ĸ�����б����ɣ���ͼ2��ʾ�����Ҫ������̨��ˮƽ��������Ϊ4�ף��µ���߳�Ϊ8�ף���б�����������ɵĽ�Ϊ![]() ��
��

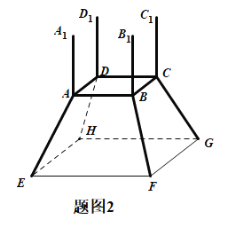
��1����![]() ��ʾ�����ϰ벿�������ĸ߶ȣ�����
��ʾ�����ϰ벿�������ĸ߶ȣ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2�����������ϰ벿�����������Ϊ![]() ǧԪ/�ף��������ֺ��Բ��ƣ����°벿�ֺ�����б������۶�Ϊ2ǧԪ/�ף��ʵ�
ǧԪ/�ף��������ֺ��Բ��ƣ����°벿�ֺ�����б������۶�Ϊ2ǧԪ/�ף��ʵ�![]() Ϊ��ֵʱ�������������ͣ�
Ϊ��ֵʱ�������������ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������һ̨ij�ͺŻ�����2�ֹ���״̬������״̬����״̬.���������ڹ���״̬����ͣ������.Ϊ�˼���������״̬�Ƿ��������������ͳ���˸û���������������״̬��������1000����Ʒ������ָ��ֵ���ó���ͼ1��ʾƵ�ʷֲ�ֱ��ͼ.��ͳ�ƽ��������Ϊ�����ֲ�Ʒ������ָ��ֵ������̬�ֲ�![]() ������
������![]() ����Ϊ��1000����Ʒ������ָ��ֵ��ƽ����
����Ϊ��1000����Ʒ������ָ��ֵ��ƽ����![]() ��
��![]() ����Ϊ��1000����Ʒ������ָ��ֵ�ķ���
����Ϊ��1000����Ʒ������ָ��ֵ�ķ���![]() ��ͬһ���е������ø��������е�ֵΪ������.����Ʒ������ָ��ֵȫ����
��ͬһ���е������ø��������е�ֵΪ������.����Ʒ������ָ��ֵȫ����![]() ֮�ڣ�����Ϊ������������״̬��������Ϊ�������ڹ���״̬.
֮�ڣ�����Ϊ������������״̬��������Ϊ�������ڹ���״̬.
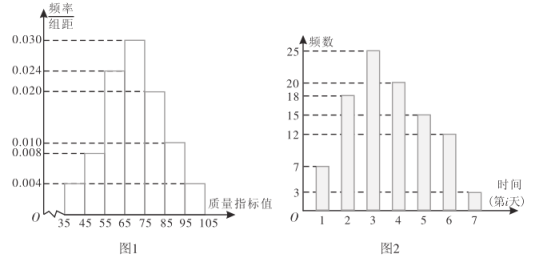
��1�������Ǽ���Ա��һ���ڴӸû��������IJ�Ʒ�������ȡ10����õ�����ָ��ֵ��
29 45 55 63 67 73 78 87 93 113
���жϸû����Ƿ���ֹ��ϣ�
��2�����������ֹ��ϣ���2�ּ������ɹ�ѡ��
����һ���Ӽ����ޣ�����˾���ڵ����ų����ϣ�����Ϊ700Ԫ��
��������������ޣ�����˾���������ڵ�����һ�����ų����ϣ�����Ϊ200Ԫ.
��������ڻ������ֹ���ʱ���ù���ѡ����ַ������м��ޣ�Ϊ���Ѽ�����˾�Ը��ͺŻ�����100����������ڵ�i��![]() ��2������7������ĵ������õ���ͼ2��ʾ��״ͼ������i�쳣���������Ƶ�ʴ������.��֪�û�����������һ�������200Ԫ�����ϻ��������첻���������������ֹ��ϣ���ѡ�����ּ�������
��2������7������ĵ������õ���ͼ2��ʾ��״ͼ������i�쳣���������Ƶ�ʴ������.��֪�û�����������һ�������200Ԫ�����ϻ��������첻���������������ֹ��ϣ���ѡ�����ּ�������
����![]() ��
��![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ǵ�2020��2��14����2020��4��19�չ�66����¹ڷ����й�/��������ȷ������ͼ�����ݸ�ͼ�����н����д�����ǣ� ��
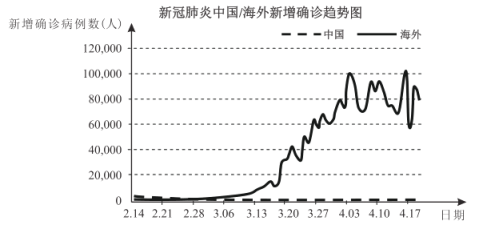
A.��2020��2��14�����й��Ѿ���������ס���ڵ��¹ڷ�������
B.��2020��3��13����2020��4��3�պ����¹ڷ���������ٶ�
C.��66�캣��ÿ�������¹ڷ���ȷ�ﲡ��������λ��������![]() ��
��
D.���������¹ڷ���ȷ�ﲡ��������һ��ͻ��10����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �У�
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() .
.
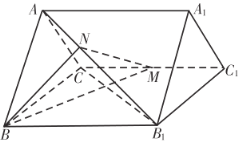
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2�������٣�ֱ��![]() ��ƽ��
��ƽ��![]() ���ɵĽ�Ϊ
���ɵĽ�Ϊ![]() ��
��
�����ڣ�![]() Ϊ��ǣ�����
Ϊ��ǣ�����![]() �����Ϊ
�����Ϊ![]() .
.
������������������ѡһ��������������������У�����������⣺
��ƽ��![]() ƽ��
ƽ��![]() ��______����ƽ��
��______����ƽ��![]() ��ƽ��
��ƽ��![]() ���ɵ������ǵ�����ֵ.
���ɵ������ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��2020��2��15����3��2���人�������¹ڷ���ȷ�ﲡ��������ͳ��ͼ��������˵������ȷ���ǣ� ��

A.2020��2��19���人�������¹ڷ���ȷ�ﲡ������½�����λ��
B.�人�����¹ڷ������������ȡ���˽��Եijɹ���������Ҫ���ܽ���
C.2020��2��19����3��2���人�������¹ڷ���ȷ�ﲡ������400�˵���8��
D.2020��2��15�յ�3��2���人�������¹ڷ���ȷ�ﲡ������һ������ٵ�һ���1549��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() �Ķ������ֵ��
�Ķ������ֵ��
��2����![]() �ĵ������䣻
�ĵ������䣻
��3����![]() �ķ�����Ϊ
�ķ�����Ϊ![]() �������x�ķ��̣�
�������x�ķ��̣�![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��˫����C�Ľ����߷���Ϊ![]() ��һ������ΪF��0����8�������˫���ߵı�����Ϊ_____.��֪��A����6��0��������PΪC��һ���㣬��P����x���Ϸ�������P��λ�ñ仯ʱ����PAF���ܳ�����СֵΪ_____.
��һ������ΪF��0����8�������˫���ߵı�����Ϊ_____.��֪��A����6��0��������PΪC��һ���㣬��P����x���Ϸ�������P��λ�ñ仯ʱ����PAF���ܳ�����СֵΪ_____.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com