
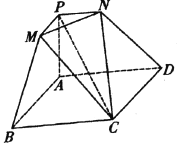
【题目】如图所示的几何体是由棱台![]() 和棱锥
和棱锥![]() 拼接而成的组合体,其底面四边形
拼接而成的组合体,其底面四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() 平面
平面![]() .
.
(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐角二面角的余弦值.
所成锐角二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)根据菱形性质得![]() ,根据线面垂直得
,根据线面垂直得![]() ,再根据线面垂直判定定理得
,再根据线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() .最后根据
.最后根据![]() 得结论,(2)先根据条件建立空间直角坐标系,设立各点坐标,根据方程组解得法向量,根据向量数量积求夹角,最后根据二面角与向量夹角关系确定所成锐角二面角的余弦值.
得结论,(2)先根据条件建立空间直角坐标系,设立各点坐标,根据方程组解得法向量,根据向量数量积求夹角,最后根据二面角与向量夹角关系确定所成锐角二面角的余弦值.
试题解析:(1)证明:因为底面四边形![]() 是菱形,
是菱形,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() , ∴
, ∴![]() 平面
平面![]() ,
,
∴![]() .
.
又棱台![]() 中,
中,![]()
∴![]()

(2)建立空间直角坐标系如图所示, 则![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则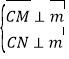 ,
,
∴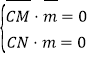 ,
,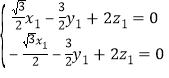 .
.
令![]() ,得
,得![]() , ∴
, ∴![]() ;
;
设平面![]() 的法向量为
的法向量为![]() ,则
,则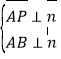 ,
,
∴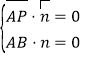 ,
,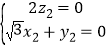
令![]() ,得
,得![]() ,
,![]() , ∴
, ∴![]() ,
,
设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,
,
则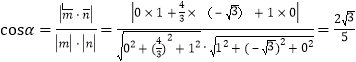 ,
,
所以平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.



 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】某兴趣小组测量电视塔AE的高度H(单位m),如示意图,垂直放置的标杆BC高度h=4m,仰角∠ABE=α,∠ADE=β

(1)该小组已经测得一组α、β的值,tanα=1.24,tanβ=1.20,,请据此算出H的值
(2)该小组分析若干测得的数据后,发现适当调整标杆到电视塔的距离d(单位m),使α与β之差较大,可以提高测量精确度,若电视塔实际高度为125m,问d为多少时,α-β最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的离心率是
的离心率是![]() ,一个顶点是
,一个顶点是![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
,![]() 是椭圆
是椭圆![]() 上异于点
上异于点![]() 的任意两点,且
的任意两点,且![]() .试问:直线
.试问:直线![]() 是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为![]() .
.
(1)请将上述列联表补充完整;
(2)并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(3)已知在被调查的学生中有5名来自甲班,其中3名喜欢游泳,现从这5名学生中随机抽取2人,求恰好有1人喜欢游泳的概率.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: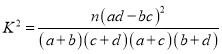 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求下列各式中x,y的值:
(1)若![]() ,则
,则![]() ______________;
______________;
(2)若![]() ,则
,则![]() ___________;
___________;
(3)若![]() ,则
,则![]() ____________;
____________;
(4)若![]() ,则
,则![]() _____________;
_____________;
(5)若![]() ,则
,则![]() ________________;
________________;
(6)若![]() ,则
,则![]() _____________,
_____________,![]() __________;
__________;
(7)若![]() ,则
,则![]() _______________.
_______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 分別为棱
分別为棱![]() 的中点
的中点

(1)求三棱柱![]() 的体积;
的体积;
(2)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在党中央的正确指导下,通过全国人民的齐心协力,特别是全体一线医护人员的奋力救治,二月份“新冠肺炎”疫情得到了控制.下图是国家卫健委给出的全国疫情通报,甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图如下:

根据图中甲、乙两省的数字特征进行比对,通过比较把你得到最重要的两个结论写在答案纸指定的空白处.
①_________________________________________________.
②_________________________________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018·长沙二模)在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外接圆面积为S2,则![]() .推广到空间可以得到类似结论:已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则
.推广到空间可以得到类似结论:已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则![]() =________.
=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com