
【题目】已知在△ABC中,角A,B,C所对的边分别为a,b,c,其中A为锐角,且asin(B+C)是![]() bcosC与
bcosC与![]() ccosB的等差中项.
ccosB的等差中项.
(1)求角A的大小;
(2)若点D在△ABC的内部,且满足∠CAD=∠ABD![]() ,∠CBD
,∠CBD![]() ,AD=1,求CD的长.
,AD=1,求CD的长.
【答案】(1)A![]() .(2)
.(2)![]() .
.
【解析】
(1)由已知得出条件等式,由正弦定理、两角和正弦公式化简,即可求出![]() ;
;
(2)根据已知条件在![]() 中,用余弦定理求出
中,用余弦定理求出![]() ,在
,在![]() 中,用正弦定理求出
中,用正弦定理求出![]() ,在
,在![]() 中,用余弦定理,求出
中,用余弦定理,求出![]() .
.
(1)∵asin(B+C)是![]() bcosC与
bcosC与![]() ccosB的等差中项.
ccosB的等差中项.
∴2asin(B+C)![]() bcosC
bcosC![]() ccosB,
ccosB,
∴可得:2sin2A![]() (sinBcosC+sinCcosB)
(sinBcosC+sinCcosB)![]() sin(B+C)
sin(B+C)![]() sinA,
sinA,
∵A为锐角,sinA≠0,
∴sinA![]() ,可得A
,可得A![]() .
.
(2)∵满足∠CAD=∠ABD![]() ,∠CBD
,∠CBD![]() ,A
,A![]() ,AD=1,
,AD=1,
∴∠BAD=∠ABD![]() ,可得AD=BD=1,∠ADB
,可得AD=BD=1,∠ADB![]() ,
,
∴在△ABD中,由余弦定理可得
AB![]()
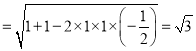 ,
,
∴∠ABC=∠ABD+∠DBC![]() ,
,
可得∠ACB=π﹣∠BAC﹣∠ABC![]() ,
,
∴△ABC中,由正弦定理![]() ,
,
可得 ,可得BC
,可得BC![]() ,
,
∴△BDC中,由余弦定理可得:
CD![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,“建设美丽中国”已成为新时代中国特色社会主义生态文明建设的重要内容,某班在一次研学旅行活动中,为了解某苗圃基地的柏树幼苗生长情况,在这些树苗中随机抽取了120株测量高度(单位:![]() ),经统计,树苗的高度均在区间
),经统计,树苗的高度均在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图.据当地柏树苗生长规律,高度不低于
分成6组,制成如图所示的频率分布直方图.据当地柏树苗生长规律,高度不低于![]() 的为优质树苗.
的为优质树苗.

(1)求图中![]() 的值;
的值;
(2)已知所抽取的这120株树苗来自于![]() ,
,![]() 两个试验区,部分数据如下列联表:
两个试验区,部分数据如下列联表:
|
| 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
将列联表补充完整,并判断是否有99.9%的把握认为优质树苗与![]() ,
,![]() 两个试验区有关系,并说明理由;
两个试验区有关系,并说明理由;
(3)通过用分层抽样方法从![]() 试验区被选中的树苗中抽取5株,若从这5株树苗中随机抽取2株,求优质树苗和非优质树苗各有1株的概率.
试验区被选中的树苗中抽取5株,若从这5株树苗中随机抽取2株,求优质树苗和非优质树苗各有1株的概率.
附:参考公式与参考数据:
其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一排组成.
| 明文字符 | A | B | C | D |
密码字符 | 11 | 12 | 13 | 14 | |
| 明文字符 | E | F | G | H |
密码字符 | 21 | 22 | 23 | 24 | |
| 明文字符 | M | N | P | Q |
密码字符 | 1 | 2 | 3 | 4 |
设随机变量![]() 表示密码中不同数字的个数.
表示密码中不同数字的个数.
(Ⅰ)求![]() 的分布列和它的数学期望.
的分布列和它的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中为了了解高三学生每天自主参加体育锻炼的情况,随机抽取了100名学生进行调查,其中女生有55名.下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图:
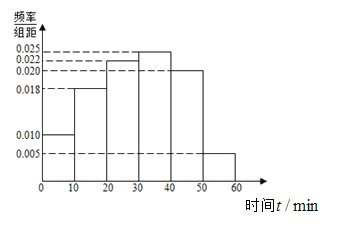
将每天自主参加体育锻炼时间不低于40分钟的学生称为体育健康A类学生,已知体育健康A类学生中有10名女生.
(Ⅰ)根据已知条件完成下面![]() 列联表,并据此资料你是否认为达到体育健康A类学生与性别有关?
列联表,并据此资料你是否认为达到体育健康A类学生与性别有关?
非体育健康A类学生 | 体育健康A类学生 | 合计 | |
男生 | |||
女生 | |||
合计 |
(Ⅱ)将每天自主参加体育锻炼时间不低于50分钟的学生称为体育健康![]() 类学生,已知体育健康
类学生,已知体育健康![]() 类学生中有2名女生,若从体育健康
类学生中有2名女生,若从体育健康![]() 类学生中任意选取2人,求至少有1名女生的概率.
类学生中任意选取2人,求至少有1名女生的概率.
附:
P( | 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
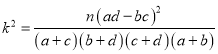
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (α为参数),曲线C2的参数方程为
(α为参数),曲线C2的参数方程为![]() (β为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
(β为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C1和C2的极坐标方程;
(2)若点A在曲线C1上,点B在曲线C2上,且∠AOB![]() ,求|OA||OB|的最大值.
,求|OA||OB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为美化校园,江苏省淮阴中学将一个半圆形的边角地改造为花园.如图所示,O为圆心,半径为1千米,点A、B、P都在半圆弧上,设∠NOP=∠POA=![]() ,∠AOB=
,∠AOB=![]() ,且
,且![]() .
.
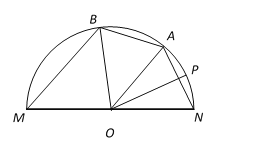
(1)请用![]() 分别表示线段NA、BM的长度;
分别表示线段NA、BM的长度;
(2)若在花园内铺设一条参观线路,由线段NA、AB、BM三部分组成,则当![]() 取何值时,参观线路最长?
取何值时,参观线路最长?
(3)若在花园内的扇形ONP和四边形OMBA内种满杜鹃花,则当![]() 取何值时,杜鹃花的种植总面积最大?
取何值时,杜鹃花的种植总面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com