
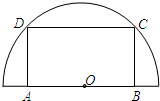
 如图,在半径为20cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.
如图,在半径为20cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.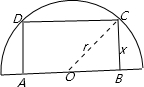 解:如图所示,
解:如图所示, );
); 时,S取最大值为900,此时BC=10
时,S取最大值为900,此时BC=10 ;
; 时,矩形ABCD的面积最大,最大值为400cm2.
时,矩形ABCD的面积最大,最大值为400cm2.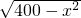 (其中0<x<30),
(其中0<x<30),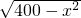 =2
=2  ≤x2+(400-x2)=400,当且仅当x2=400-x2,即x=10
≤x2+(400-x2)=400,当且仅当x2=400-x2,即x=10  时,S取最大值400;
时,S取最大值400; cm时,矩形ABCD的面积最大,最大值为400cm2.
cm时,矩形ABCD的面积最大,最大值为400cm2. 时,得到C点,从而截得的矩形ABCD,此时截得的矩形ABCD的面积最大,最大值为400cm2.
时,得到C点,从而截得的矩形ABCD,此时截得的矩形ABCD的面积最大,最大值为400cm2.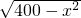 =2
=2  ,由基本不等式可得S的最大值以及对应的x的取值;
,由基本不等式可得S的最大值以及对应的x的取值;

科目:高中数学 来源: 题型:
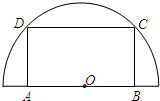 (2013•闵行区二模)如图,在半径为20cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.
(2013•闵行区二模)如图,在半径为20cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.查看答案和解析>>
科目:高中数学 来源:黄冈新内参·高考(专题)模拟测试卷·数学 题型:044
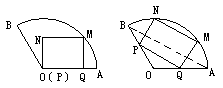
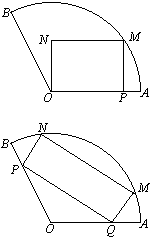
将一块圆心角为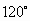 ,半径为20cm的扇形铁片裁成一块矩形,如下图所示有两种裁法:(让矩形一边在扇形的一条半径OA上,如图(1);或让矩形一边与扇形的弦AB平行,如图(2),请问哪一种裁法能得到最大面积的矩形?并求出这个最大值.
,半径为20cm的扇形铁片裁成一块矩形,如下图所示有两种裁法:(让矩形一边在扇形的一条半径OA上,如图(1);或让矩形一边与扇形的弦AB平行,如图(2),请问哪一种裁法能得到最大面积的矩形?并求出这个最大值.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
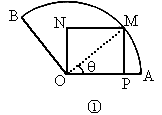
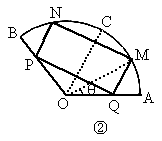
将一块圆心角为120°,半径为20cm的扇形铁片裁成一块矩形,如图所示,有两种裁法:让矩形一边在扇形的一条半径OA上,或让矩形一边与弦AB平行,试问哪种裁法能得到矩形的面积最大,并求出这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com