
【题目】已知函数![]()
(1)求![]() 的最小正周期;
的最小正周期;
(2)设![]() 为锐角三角形,角A的对边长
为锐角三角形,角A的对边长![]() 角B的对边长
角B的对边长![]() 若
若![]() 求
求![]() 的面积.
的面积.
【答案】(1)π(2)![]()
【解析】
(1)利用三角恒等变换化简函数的解析式,再根据正弦函数的周期性,得出结论.
(2)根据f(A)=0,求得A的值,再利用正弦定理求得B,可得C的值,利用△ABC的面积为 ![]() absinC,计算求得结果.
absinC,计算求得结果.
解:(1)函数f(x)=sinxcosx﹣sin2x=![]() sin2x﹣
sin2x﹣![]() =
=![]() sin(2x+
sin(2x+![]() )﹣
)﹣![]() ,
,
故它的最小正周期为![]() =π.
=π.
(2)∵△ABC为锐角三角形,角A的对边长![]() ,角B的对边长
,角B的对边长![]() ,
,
若f(A)=![]() sin(2A+
sin(2A+![]() )﹣
)﹣![]() =0,
=0,
∴sin(2A+![]() )=
)=![]() ,∴2A+
,∴2A+![]() =
=![]() ,∴A=
,∴A=![]() .
.
再由正弦定理可得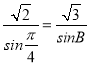 ,∴sinB=
,∴sinB=![]() ,
,
∴B=![]() ,∴C=π﹣A﹣B=
,∴C=π﹣A﹣B=![]() ,
,
∴sinC=sin(![]() +
+![]() )=sin
)=sin![]() cos
cos![]() +cos
+cos![]() sin
sin![]() =
=![]() =
=![]() ,
,
故△ABC的面积为 ![]() absinC=
absinC=![]()
![]()
![]()
![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】我们把定义在![]() 上,且满足
上,且满足![]() (其中常数
(其中常数![]() ,
,![]() 满足
满足![]() ,
,![]() ,
,![]() )的函数叫做似周期函数.
)的函数叫做似周期函数.
(1)若某个似周期函数![]() 满足
满足![]() 且图像关于直线
且图像关于直线![]() 对称,求证:函数
对称,求证:函数![]() 是偶函数;
是偶函数;
(2)当![]() ,
,![]() 时,某个似周期函数在
时,某个似周期函数在![]() 时的解析式为
时的解析式为![]() ,求函数
,求函数![]() ,
,![]() 的解析式;
的解析式;
(3)对于确定的![]() 且当
且当![]() 时,
时,![]() ,试研究似周期函数
,试研究似周期函数![]() 在区间
在区间![]() 上是否可能是单调函数?若可能,求出
上是否可能是单调函数?若可能,求出![]() 的取值范围;若不可能,请说明理由.
的取值范围;若不可能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问100名性别不同的大学生是否爱好某项运动,得到如下![]() 列联表:
列联表:
(1)能否有![]() 的把握认为是否爱好该项运动与性别有关?请说明理由.
的把握认为是否爱好该项运动与性别有关?请说明理由.
(2)利用分层抽样的方法从以上爱好该项运动的大学生中抽取6人组建“运动达人社”,现从“运动达人社”中选派2人参加某项校际挑战赛,求选出的2人中恰有1名女大学生的概率.
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 15 | 25 | 40 |
总计 | 55 | 45 | 100 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
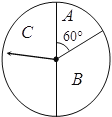
(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图的折线图是某超市2018年一月份至五月份的营业额与成本数据,根据该折线图,下列说法正确的是( )
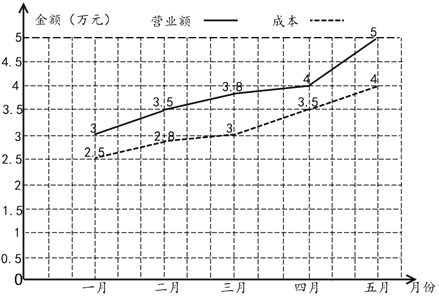
A.该超市2018年的前五个月中三月份的利润最高
B.该超市2018年的前五个月的利润一直呈增长趋势
C.该超市2018年的前五个月的利润的中位数为0.8万元
D.该超市2018年前五个月的总利润为3.5万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,点
,点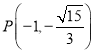 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,使得
两点,使得![]() ?若存在,求出直线的方程;若不存在,说明理由.
?若存在,求出直线的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com