Question

8．若实数x，y满足$\left\{\begin{array}{l}{y≤2}\\{|x|-y+1≤0}\end{array}\right.$，则z=$\frac{y+2}{x-2}$的最小值为4．

Answer 1

分析 作出题中不等式组表示的平面区域，得到如图的△ABC及其内部．设Q（x，y）为区域内一点，定点P（2，-2），可得目标函数z表示P、Q两点连线的斜率，运动点Q并观察直线PQ斜率的变化，即可得到z的最小值．

解答 解：由题意作平面区域如下：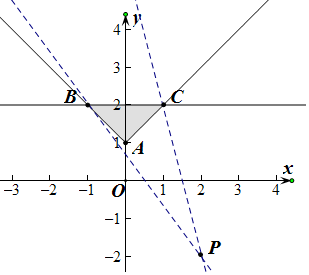

得到如图的△ABC及其内部，
其中A（0，1），B（-1，2），C（1，2），
设Q（x，y）为区域内一个动点，定点P（2，-2）．
可得z=$\frac{y+2}{x-2}$的几何意义是表示P、Q两点连线的斜率，
运动点Q，可得当Q与C重合时，k_PQ=$\frac{2+2}{1-2}$=-4达到最小值，
即z的最小值是-4，
故答案为：-4

点评 本题给出二元一次不等式组，求目标函数z的最小值，着重考查了二元一次不等式组表示的平面区域和直线的斜率等知识，属于基础题．