
【题目】设常数![]() ,函数
,函数![]() .
.
(1) 若![]() ,求
,求![]() 的单调递减区间;
的单调递减区间;
(2) 若![]() 为奇函数,且关于
为奇函数,且关于![]() 的不等式
的不等式![]() 对所有的
对所有的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3) 当![]() 时,若方程
时,若方程![]() 有三个不相等的实数根
有三个不相等的实数根![]() 、
、![]() 、
、![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1) ![]() 的单调递减区间为
的单调递减区间为![]() 和
和![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]()
【解析】
(1)去绝对值符号后画出函数的图像,从而得到函数的单调减区间.
(2)根据函数为奇函数可得![]() ,再利用
,再利用![]() 去掉绝对值符号,最后参变分离求
去掉绝对值符号,最后参变分离求![]() 的取值范围.
的取值范围.
(3)先去掉绝对值符号,画出函数图像,因为![]() 有三个不同的解,可以得到其中有两个根的和为
有三个不同的解,可以得到其中有两个根的和为![]() ,再利用求根公式求出最大根,从而得到关于
,再利用求根公式求出最大根,从而得到关于![]() 的方程,解方程可得
的方程,解方程可得![]() 的值.
的值.
(1) 当![]() 时,
时,![]() .如图知,
.如图知,![]() 的单调递减区间为
的单调递减区间为![]() 和
和![]() .
.

(2) 由![]() 为奇函数,得
为奇函数,得![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() .
.
从而![]() ,
,![]() .
.
又![]() 在
在![]() 上递增,故当
上递增,故当![]() 时,
时,![]() .故
.故![]() .
.
(3)当![]() 时,
时,![]() .
.

如图,![]() 要有三个不相等的实根,则
要有三个不相等的实根,则![]() ,解得
,解得![]() .
.
不妨设![]() ,当
,当![]() 时,由
时,由![]() ,即
,即![]() ,得
,得![]() .
.
当![]() 时,由
时,由![]() ,即
,即![]() ,得
,得![]() .
.
由![]() ,解得
,解得![]() .
.
因![]() ,得
,得![]() 的值为
的值为![]() .
.


科目:高中数学 来源: 题型:
【题目】为了让观赏游玩更便捷舒适,常州恐龙园推出了代步工具租用服务.已知有脚踏自行车![]() 与电动自行车
与电动自行车![]() 两种车型,采用分段计费的方式租用.
两种车型,采用分段计费的方式租用.![]() 型车每
型车每![]() 分钟收费
分钟收费![]() 元(不足
元(不足![]() 分钟的部分按
分钟的部分按![]() 分钟计算),
分钟计算),![]() 型车每
型车每![]() 分钟收费
分钟收费![]() 元(不足
元(不足![]() 分钟的部分按
分钟的部分按![]() 分钟计算),现有甲乙丙丁四人,分别相互独立地到租车点租车骑行(各租一车一次),设甲乙丙丁不超过
分钟计算),现有甲乙丙丁四人,分别相互独立地到租车点租车骑行(各租一车一次),设甲乙丙丁不超过![]() 分钟还车的概率分别为
分钟还车的概率分别为![]() ,并且四个人每人租车都不会超过
,并且四个人每人租车都不会超过![]() 分钟,甲乙丙均租用
分钟,甲乙丙均租用![]() 型车,丁租用
型车,丁租用![]() 型车.
型车.
(1)求甲乙丙丁四人所付的费用之和为25元的概率;
(2)求甲乙丙三人所付的费用之和等于丁所付的费用的概率;
(3)设甲乙丙丁四人所付费用之和为随机变量![]() ,求
,求![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下关于线性回归的判断,正确的个数是( )

①若散点图中所有点都在一条直线附近,则这条直线为回归直线;
②散点图中的绝大多数都线性相关,个别特殊点不影响线性回归,如图中的A,B,C点;
③已知直线方程为![]() =0.50x-0.81,则x=25时,y的估计值为11.69;
=0.50x-0.81,则x=25时,y的估计值为11.69;
④回归直线方程的意义是它反映了样本整体的变化趋势.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +x.
+x.
(1)若函数f(x)的图象在(1,f(1))处的切线经过点(0,﹣1),求a的值;
(2)是否存在负整数a,使函数f(x)的极大值为正值?若存在,求出所有负整数a的值;若不存在,请说明理由;
(3)设a>0,求证:函数f(x)既有极大值,又有极小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={a1 , a2 , …,am}.若集合A1∪A2∪A3∪…∪An=A,则称A1 , A2 , A3 , …,An为集合A的一种拆分,所有拆分的个数记为f(n,m).
(1)求f(2,1),f(2,2),f(3,2)的值;
(2)求f(n,2)(n≥2,n∈N*)关于n的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=![]() AD,E,F分别为线段AD,PC的中点.
AD,E,F分别为线段AD,PC的中点.

(1)求证:AP∥平面BEF;
(2)求证:BE⊥平面PAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
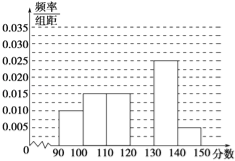
(1)求分数在[120,130)内的频率;
(2)若在同一组数据中,将该组区间的中点值(如:组区间[100,110)的中点值为![]() =105)作为这组数据的平均分,据此,估计本次考试的平均分;
=105)作为这组数据的平均分,据此,估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据:

(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测技改后生产100吨甲产品比技改前少消耗多少吨标准煤.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|﹣|x﹣3|.
(Ⅰ)解不等式f(x)≥1;
(Ⅱ)当﹣9≤x≤4时,不等式f(x)<a成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com