

A. | B. | C. | D. |
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源:不详 题型:解答题
 ,四边形ACFE是矩形,且平面
,四边形ACFE是矩形,且平面 平面ABCD,点M在线段EF上.
平面ABCD,点M在线段EF上. 平面ACFE;
平面ACFE;
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.过a一定存在平面β,使得β∥α |
| B.过a一定存在平面β,使得β⊥α |
| C.在平面α内一定不存在直线b,使得a⊥b |
| D.在平面α内一定不存在直线b,使得a∥b |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段 上,且
上,且 ,设面
,设面 面MPQ=
面MPQ= ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )
 面ABCD
面ABCD AC
AC 不是定直线
不是定直线查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 平面
平面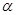 ,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,则线段AB与EF在平面
,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,则线段AB与EF在平面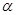 上的射影所成角余弦值的范围是( )
上的射影所成角余弦值的范围是( )A.[0, ] ] | B.[ ,1] ,1] | C.[ ,1] ,1] | D.[ , , ] ] |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的棱长为1,P为BC的中点,Q为线段
的棱长为1,P为BC的中点,Q为线段 上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是__ ___(写出所有正确命题的编号).
上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是__ ___(写出所有正确命题的编号).
 时,S为四边形;
时,S为四边形;  时,S不为等腰梯形;
时,S不为等腰梯形; 时,S与
时,S与 的交点R满足
的交点R满足 ;
; 时,S为六边形;
时,S为六边形; 时,S的面积为
时,S的面积为 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com