
【题目】如图,直线AB经过☉O上的点C,并且OA=OB,CA=CB,☉O交直线OB于E,D两点,连接EC,CD. 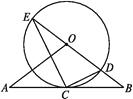
(1)求证:直线AB是☉O的切线;
(2)若tan∠CED= ![]() ,☉O的半径为3,求OA的长.
,☉O的半径为3,求OA的长.
【答案】
(1)证明:如图,连接OC,
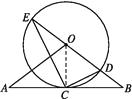
∵OA=OB,CA=CB,
∴OC⊥AB.
∴AB是☉O的切线.
(2)解:∵ED是直径,
∴∠ECD=90°.
∴在Rt△ECD中,tan∠CED= .
∵BC是☉O的切线,
∴BC2=BD·BE,∠BCD=∠E.
又∠CBD=∠EBC,
∴△BCD∽△BEC.
∴ ![]() .
.
设OA=x,则BD=OB-OD=x-3,BC=2BD=2(x-3),BE=BO+OE=x+3,
∴[2(x-3)]2=(x-3)(x+3),
解得x=5或x=3(舍去).
∴OA=5.
【解析】本题主要考查了与圆有关的比例线段,解决问题的关键是:(1)转化为证明OC⊥AB即可;(2)先证明△BCD∽△BEC,再借助于对应边成比例,解方程得OA的长


科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|2x﹣1|+|x+1|,g(x)=|x﹣a|+|x+a|.
(Ⅰ)解不等式f(x)>9;
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2),求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,圆锥SO的轴截面△SAB是边长为4的正三角形,M为母线SB的中点,过直线AM作平面β⊥面SAB,设β与圆锥侧面的交线为椭圆C,则椭圆C的短半轴长为( ) 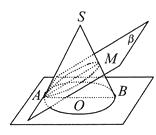
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间; 
(2)写出函数f(x)的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行,依此类推,則第20行从左至右的第4个数字应是 . 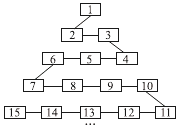
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①直线l的方向向量为 ![]() =(1,﹣1,2),直线m的方向向量
=(1,﹣1,2),直线m的方向向量 ![]() =(2,1,﹣
=(2,1,﹣ ![]() ),则l与m垂直;
),则l与m垂直;
②直线l的方向向量 ![]() =(0,1,﹣1),平面α的法向量
=(0,1,﹣1),平面α的法向量 ![]() =(1,﹣1,﹣1),则l⊥α;
=(1,﹣1,﹣1),则l⊥α;
③平面α、β的法向量分别为 ![]() =(0,1,3),
=(0,1,3), ![]() =(1,0,2),则α∥β;
=(1,0,2),则α∥β;
④平面α经过三点A(1,0,﹣1),B(0,1,0),C(﹣1,2,0),向量 ![]() =(1,u,t)是平面α的法向量,则u+t=1.
=(1,u,t)是平面α的法向量,则u+t=1.
其中真命题的是 . (把你认为正确命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com