
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并解答.
①![]()
②![]()
③![]() 的面积为
的面积为![]()
在![]() 中,内角A,B,C所对的边分别为a,b,c,已知b-c=2,cosA=
中,内角A,B,C所对的边分别为a,b,c,已知b-c=2,cosA=![]() , .
, .
(1)求a;
(2)求![]() 的值.
的值.
【答案】(1)不论选哪种条件,a=8(2)![]()
【解析】
方案一:选择条件①:(1)首先利用向量的加法以及向量的数量积可得![]() ,从而可求出
,从而可求出![]() 、
、![]() ,然后再利用余弦定理即可求解.
,然后再利用余弦定理即可求解.
(2)利用余弦定理可得![]() ,再利用同角三角函数的基本关系求出
,再利用同角三角函数的基本关系求出![]() ,由二倍角公式以及两角和的余弦公式即可求解.
,由二倍角公式以及两角和的余弦公式即可求解.
方案二:选择条件②:(1)求出![]() 、
、![]() ,再利用余弦定理即可求解.
,再利用余弦定理即可求解.
(2)同方案一
方案三:选择条件③:(1)利用同角三角函数的基本关系求出![]() ,再利用三角形的面积公式可得
,再利用三角形的面积公式可得![]() ,求出
,求出![]() 、
、![]() ,再利用余弦定理即可求解.
,再利用余弦定理即可求解.
(2)同方案一.
解:方案一:选择条件①:
(1)![]()
![]()
∵![]()
∴bc=24
由![]() 解得
解得![]() 或
或![]() (舍去)
(舍去)
∴![]()
∴a=8
(2)![]()
![]()
![]()
∴![]()
∴![]()
![]()
∴![]()
![]()
方案二:选择条件②:
(1)由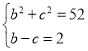 解得
解得![]() 或
或![]() (舍去)
(舍去)
∴![]()
∴a=8
(2)同方案一
方案三:选择条件③:
(1)∵![]()
∴![]()
![]()
∴bc=24
由![]() 解得
解得![]() 或
或![]() (舍)
(舍)
∴![]()
∴a=8
(2)同方案一.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (
(![]() )的焦点为
)的焦点为![]() ,以原点O为圆心,椭圆E的短半轴长为半径的圆与直线
,以原点O为圆心,椭圆E的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆E的方程;
(2)过点F的直线l交椭圆E于M,N两点,点P的坐标为![]() ,直线
,直线![]() 与x轴交于A点,直线
与x轴交于A点,直线![]() 与x轴交于B点,求证:
与x轴交于B点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】著名物理学家李政道说:“科学和艺术是不可分割的”.音乐中使用的乐音在高度上不是任意定的,它们是按照严格的数学方法确定的.我国明代的数学家、音乐理论家朱载填创立了十二平均律是第一个利用数学使音律公式化的人.十二平均律的生律法是精确规定八度的比例,把八度分成13个半音,使相邻两个半音之间的频率比是常数,如下表所示,其中![]() 表示这些半音的频率,它们满足
表示这些半音的频率,它们满足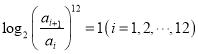 .若某一半音与
.若某一半音与![]() 的频率之比为
的频率之比为![]() ,则该半音为( )
,则该半音为( )
频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
半音 | C |
| D |
| E | F |
| G |
| A |
| B | C(八度) |
A.![]() B.GC.
B.GC.![]() D.A
D.A
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一条曲线C在y轴右侧,曲线C上任意一点到点![]() 的距离减去它到y轴的距离都等于1.
的距离减去它到y轴的距离都等于1.
(1)求曲线C的方程;
(2)直线![]() 与轨迹C交于A,B两点,问:在x轴上是否存在定点
与轨迹C交于A,B两点,问:在x轴上是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 关于x轴对称而与直线
关于x轴对称而与直线![]() 的位置无关,若存在,求出点M的坐标,若不存在,请说明理由.
的位置无关,若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,左右顶点分别为
,左右顶点分别为![]() 、
、![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() (不与
(不与![]() 轴重合)交椭圆
轴重合)交椭圆![]() 于
于![]() 、
、![]() 点,直线
点,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() .
.
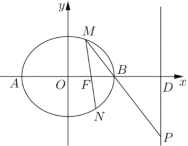
(1)求椭圆![]() 的方程;
的方程;
(2)若![]()
![]() ,求出点
,求出点![]() 的坐标;
的坐标;
(3)求证:![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 有两个不同的零点
有两个不同的零点![]() .
.
(ⅰ)求实数![]() 的取值范围;
的取值范围;
(ⅱ)求证:![]() .(其中
.(其中![]() 为
为![]() 的极小值点)
的极小值点)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com