
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源:不详 题型:单选题
| A.(-∞,2) | B.(4,+∞) |
| C.(-∞,2)∪(4,+∞) | D.(2,4) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
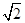 +
+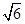 )km,∠AOB=75°,∠AOC=45°,现规划在公路l1,l2上分别选择A,B两处为交汇点(异于点O)直接修建一条公路通过C城.设OA=x km,OB=y km.
)km,∠AOB=75°,∠AOC=45°,现规划在公路l1,l2上分别选择A,B两处为交汇点(异于点O)直接修建一条公路通过C城.设OA=x km,OB=y km.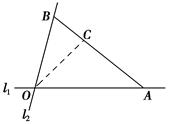
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com