
【题目】如图所示,在三棱柱ABC﹣A1B1C1中,AA1⊥底面A1B1C1 , 底面为直角三角形,∠ACB=90°,AC=2,BC=1,CC1= ![]() ,P是BC1上一动点,则A1P+PC的最小值是 .
,P是BC1上一动点,则A1P+PC的最小值是 . 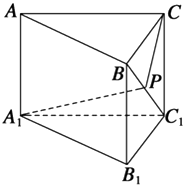
【答案】![]()
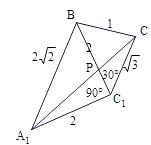
【解析】解:连A1B,沿BC1将△CBC1展开与△A1BC1在同一个平面内,如图所示, 连A1C,则A1C的长度就是所求的最小值.
在三棱柱ABC﹣A1B1C1中,AA1⊥底面A1B1C1 , 底面为直角三角形,∠ACB=90°,AC=2,BC=1,CC1= ![]() ,
,
∴BC1=2,A1C1=2,A1B=2 ![]() ,BC=1,CC1=
,BC=1,CC1= ![]() ,
,
即∠A1C1B=90°,∠CC1B=30°,
∴∠A1C1C=90°+30°=120°,
由余弦定理可求得A1C2= ![]() =
= ![]() ,
,
∴A1P+PC的最小值是 ![]() ,
,
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解棱柱的结构特征的相关知识,掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)是(﹣∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( ) 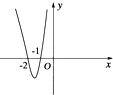
A.(﹣2,﹣1)∪(1,2)
B.(﹣2,﹣1)∪(0,1)∪(2,+∞)
C.(﹣∞,﹣2)∪(﹣1,0)∪(1,2)
D.(﹣∞,﹣2)∪(﹣1,0)∪(0,1)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
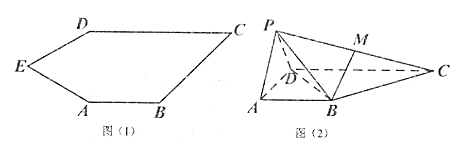
【题目】如图(1)五边形![]() 中,
中, ![]()
![]() ,将
,将![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() ,如图(2),点
,如图(2),点![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若四棱柱![]() 的体积为
的体积为![]() ,求四面体
,求四面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
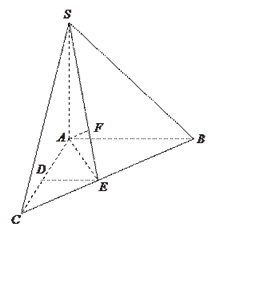
【题目】如图,在三棱锥![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,
的中点, ![]() 在
在![]() 上,且
上,且![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)在线段上![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角
![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com