
已知动圆与圆B:x2+y2-4y-32=0内切且过定点A(0,-2),求动圆圆心M的轨迹方程.
科目:高中数学 来源:江西省上饶市2012届高三第二次模拟考试数学理科试题 题型:044
已知:圆C:x2+(y-a)2=a2(a>0),动点A在x轴上方,圆A与x轴相切,且与圆C外切于点M.
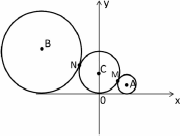
(1)若动点A的轨迹为曲线E,求曲线E的方程;
(2)动点B也在x轴上方,且A,B分别在y轴两侧.圆B与x轴相切,且与圆C外切于点N.若圆A,圆C,圆B的半径成等比数列,求证:A,C,B三点共线;
(3)在(2)的条件下,过A,B两点分别作曲线E的切线,两切线相交于点T,若![]() 的最小值为2,求直线AB的方程.
的最小值为2,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源:《第2章 圆锥曲线与方程》2010年单元测试卷(3)(解析版) 题型:解答题
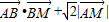 =0,求动点M的轨迹Q;
=0,求动点M的轨迹Q;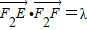 ,且λ∈[
,且λ∈[ ,1]时,求△F2CD的面积S的取值范围.
,1]时,求△F2CD的面积S的取值范围.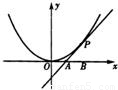
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省绵阳市三台中学高三(下)第一次月考数学试卷(文科)(解析版) 题型:解答题
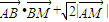 =0,求动点M的轨迹Q;
=0,求动点M的轨迹Q; ,且λ∈[
,且λ∈[ ,1]时,求△F2CD的面积S的取值范围.
,1]时,求△F2CD的面积S的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com