
【题目】某金店用一杆不准确的天平(两边臂不等长)称黄金,某顾客要购买![]() 黄金,售货员先将
黄金,售货员先将![]() 的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将
的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将![]() 的砝码放入右盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金( )
的砝码放入右盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金( )
A. 大于![]() B. 小于
B. 小于![]() C. 大于等于
C. 大于等于![]() D. 小于等于
D. 小于等于![]()
科目:高中数学 来源: 题型:
【题目】某校高三学生体检后,为了解高三学生的视力情况,该校从高三六个班的300名学生中以班为单位(每班学生50人),每班按随机抽样方法抽取了8名学生的视力数据.其中高三(1)班抽取的8名学生的视力数据与人数见下表:
视力数据 | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 | 5.1 | 5.2 | 5.3 |
人数 | 2 | 2 | 2 | 1 | 1 |
(1)用上述样本数据估计高三(1)班学生视力的平均值;
(2)已知其余五个班学生视力的平均值分别为4.3、4.4、4.5、4.6、4.8.若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() 为下述条件的函数
为下述条件的函数![]() 的集合:①定义域为
的集合:①定义域为![]() ;②对任意实数
;②对任意实数![]() ,都有
,都有![]() .
.
(1)判断函数![]() 是否为
是否为![]() 中元素,并说明理由;
中元素,并说明理由;
(2)若函数![]() 是奇函数,证明:
是奇函数,证明:![]() ;
;
(3)设![]() 和
和![]() 都是
都是![]() 中的元素,求证:
中的元素,求证: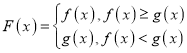 也是
也是![]() 中的元素,并举例说明,
中的元素,并举例说明,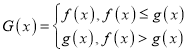 不一定是
不一定是![]() 中的元素.
中的元素.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为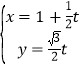 (
(![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直线
.若直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】无穷数列![]()
![]() ,若存在正整数
,若存在正整数![]() ,使得该数列由
,使得该数列由![]() 个互不相同的实数组成,且对于任意的正整数
个互不相同的实数组成,且对于任意的正整数![]() ,
,![]() 中至少有一个等于
中至少有一个等于![]() ,则称数列
,则称数列![]() 具有性质
具有性质![]() .集合
.集合![]() .
.
(1)若![]() ,
,![]() ,判断数列
,判断数列![]() 是否具有性质
是否具有性质![]() ;
;
(2)数列![]() 具有性质
具有性质![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)数列![]() 具有性质
具有性质![]() ,对于
,对于![]() 中的任意元素
中的任意元素![]() ,
,![]() 为第
为第![]() 个满足
个满足![]() 的项,记
的项,记![]()
![]() ,证明:“数列
,证明:“数列![]() 具有性质
具有性质![]() ”的充要条件为“数列
”的充要条件为“数列![]() 是周期为
是周期为![]() 的周期数列,且每个周期均包含
的周期数列,且每个周期均包含![]() 个不同实数”.
个不同实数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校![]() 名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是
名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
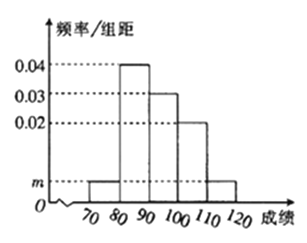
![]() 求图中
求图中![]() 的值;
的值;
![]() 根据频率分布直方图,估计这
根据频率分布直方图,估计这![]() 名学生的平均分;
名学生的平均分;
![]() 若这
若这![]() 名学生的数学成绩中,某些分数段的人数
名学生的数学成绩中,某些分数段的人数![]() 与英语成绩相应分数段的人数
与英语成绩相应分数段的人数![]() 之比如表所示,求英语成绩在
之比如表所示,求英语成绩在![]() 的人数.
的人数.
分数段 |
|
|
|
|
| 1:2 | 1:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是国际田联的标准400米跑道,它的最内侧跑道的边线是由两根84.39米的平行直线和两段半径36.80米的半圆组成,每根跑道宽1.22米(道与道间的划线宽度忽略不计).比赛时运动员从下方标有数字处出发.为了比賽公平,外道的运动员的起跑点较内道的会有一定的提前量,使得所有运动员跑过的路程完全一致.假设每位运动员都会沿着自己道次的最内侧跑.
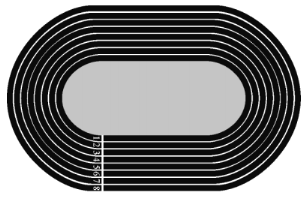
(1)试给出400米比赛各道次提前量![]() 关于道次
关于道次![]() 之间的函数关系,并完成下表(精确到0.01米)
之间的函数关系,并完成下表(精确到0.01米)
(2)800米比赛的规则是从出发处按道次跑完第一个弯道后可以开始并道赛跑,请你设计第8道选手的最优跑步路线并给出他起跑的提前量应该是多少.
道次 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
提前量(米) | 7.67 | 15.33 | 23.00 | 30.66 | 38.33 | 46.00 | 53.66 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com