
ЎѕМвДїЎїДіЦРС§Т»О»ёЯИэ°аЦчИО¶Ф±ѕ°а50ГыС§ЙъС§П°»эј«РФєН¶Фґэ°ај¶№¤ЧчµДМ¬¶ИЅшРРµчІйЈ¬µГµЅµДНіјЖКэѕЭИзПВ±нЛщКѕЈє
»эј«ІОјУ°ај¶№¤Чч | І»»эј«ІОјУ°ај¶№¤Чч | єПјЖ | |
С§П°»эј«РФёЯ | 18 | 7 | 25 |
С§П°»эј«РФІ»ёЯ | 6 | 19 | 25 |
єПјЖ | 24 | 26 | 50 |
ЈЁ1Ј©Из№ыЛж»ъµчІйХвёц°аµДТ»ГыС§ЙъЈ¬ДЗГґійµЅІ»»эј«ІОјУ°ај¶№¤ЧчЗТС§П°»эј«РФІ»ёЯµДС§ЙъµДёЕВККЗ¶аЙЩЈї
ЈЁ2Ј©ИфІ»»эј«ІОјУ°ај¶№¤ЧчЗТС§П°»эј«РФёЯµД7ГыС§ЙъЦРУРБЅГыДРЙъЈ¬ПЦґУЦРійИЎБЅГыС§ЙъІОјУДіПо»о¶ЇЈ¬ОКБЅГыС§ЙъЦРЗЎУР1ГыДРЙъµДёЕВККЗ¶аЙЩЈї
ЈЁ3Ј©КЗ·сУР![]() °СОХИПОЄС§ЙъµДС§П°»эј«РФУл¶Фґэ°ај¶№¤ЧчµДМ¬¶ИКЗ·сУР№ШПµЈїЗлЛµГчАнУЙЈ®
°СОХИПОЄС§ЙъµДС§П°»эј«РФУл¶Фґэ°ај¶№¤ЧчµДМ¬¶ИКЗ·сУР№ШПµЈїЗлЛµГчАнУЙЈ®
ёЅЈєІОїјКэѕЭЈє
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
![]() Ј¬ЖдЦР
Ј¬ЖдЦР![]()
Ўѕґр°ёЎїЈЁ1Ј©![]() Ј»ЈЁ2Ј©
Ј»ЈЁ2Ј©![]() Ј»ЈЁ3Ј©УР.
Ј»ЈЁ3Ј©УР.
ЎѕЅвОцЎї
ЈЁ1Ј©Лж»ъµчІйХвёц°аµДТ»ГыС§ЙъЈ¬УР50ЦЦЗйїцЈ¬ійµЅІ»»эј«ІОјУ°ај¶№¤ЧчЗТС§П°»эј«РФІ»ёЯµДС§ЙъЈ¬УР19ЦЦЗйїцЈ¬јґїЙЗуіцёЕВКЈ»
ЈЁ2Ј©АыУГБРѕЩ·ЁИ·¶Ё»щ±ѕКВјюµДёцКэЈ¬јґїЙЗуіцБЅГыС§ЙъЦРУР1ГыДРЙъµДёЕВКЈ»
ЈЁ3Ј©ЗуіцK2Ј¬УлБЩЅзЦµ±ИЅПЈ¬јґїЙµГіцЅбВЫЈ®
ЈЁ1Ј©Лж»ъµчІйХвёц°аµДТ»ГыС§ЙъЈ¬УР50ЦЦЗйїцЈ¬ійµЅІ»»эј«ІОјУ°ај¶№¤ЧчЗТС§П°»эј«РФІ»ёЯµДС§ЙъЈ¬УР19ЦЦЗйїцЈ¬№КёЕВККЗ![]() .
.
ЈЁ2Ј©ЙиХв7ГыС§ЙъОЄaЈ¬bЈ¬cЈ¬dЈ¬eЈ¬AЈ¬BЈЁґуРґОЄДРЙъЈ©Ј¬ФтґУЦРійИЎБЅГыС§ЙъµДЛщУР»щ±ѕКВјюКЗЈєabЈ¬acЈ¬adЈ¬aeЈ¬aAЈ¬aBЈ¬bcЈ¬bdЈ¬beЈ¬bAЈ¬BbЈ¬cdЈ¬ceЈ¬cAЈ¬cBЈ¬deЈ¬dAЈ¬dBЈ¬eAЈ¬eBЈ¬ABЈ¬№І21ёцЈ¬
ЙиЖдЦРЗЎє¬УРТ»ГыДРЙъОЄКВјюMЈ¬ФтMЦРµД»щ±ѕКВјюУР10ёцЈ¬·Ц±рОЄaAЈ¬aBЈ¬bAЈ¬BbЈ¬ cAЈ¬cBЈ¬ dAЈ¬dBЈ¬eAЈ¬eBЈ¬
ЎаЛщЗуёЕВК![]() Ј®
Ј®
ЈЁ3Ј©ёщѕЭ![]()
ЎаОТГЗУР99.9%°СОХИПОЄЎ°С§ЙъµДС§П°»эј«РФУл¶Фґэ°ај¶№¤ЧчµДМ¬¶ИЎ±УР№ШПµЈ®


 Т»ЕµКйТµКојЩЧчТµїмАЦјЩЖЪФЖДПГАКхіц°жЙзПµБРґр°ё
Т»ЕµКйТµКојЩЧчТµїмАЦјЩЖЪФЖДПГАКхіц°жЙзПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() Ј¬
Ј¬![]() .
.
ЈЁўсЈ©Иф![]() Ј¬ЅвІ»µИКЅ
Ј¬ЅвІ»µИКЅ![]() Ј»
Ј»
ЈЁўтЈ©ИфІ»µИКЅ![]() ЦБЙЩУРТ»ёцёєКэЅвЈ¬ЗуКµКэ
ЦБЙЩУРТ»ёцёєКэЅвЈ¬ЗуКµКэ![]() µДИЎЦµ·¶О§.
µДИЎЦµ·¶О§.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄФІ![]() µДФІРДФЪЦ±ПЯ
µДФІРДФЪЦ±ПЯ![]() ЙПЈ¬ЗТФІ
ЙПЈ¬ЗТФІ![]() ѕ№эµг
ѕ№эµг![]() .
.
ЈЁ1Ј©ЗуФІµД±кЧј·ЅіМЈ»
ЈЁ2Ј©Ц±ПЯ![]() №эµг
№эµг![]() ЗТУлФІ
ЗТУлФІ![]() ПаЅ»Ј¬ЛщµГПТі¤ОЄ4Ј¬ЗуЦ±ПЯ
ПаЅ»Ј¬ЛщµГПТі¤ОЄ4Ј¬ЗуЦ±ПЯ![]() µД·ЅіМ.
µД·ЅіМ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіµҐО»ѕц¶ЁН¶ЧК3200ФЄЅЁТ»ІЦївЈЁі¤·ЅМеЧґЈ©Ј¬ёЯ¶Иєг¶ЁЈ¬ЛьµДєуЗЅАыУГѕЙЗЅІ»»ЁЗ®Ј¬ХэГжУГМъХ¤Ј¬ГїГЧі¤ФмјЫ40ФЄЈ¬БЅІаЗЅЖцЧ©Ј¬ГїГЧі¤ФмјЫ45ФЄЈ¬¶ҐІїГїЖЅ·ЅГЧФмјЫ20ФЄЈ¬ЗуЈє
ЈЁ1Ј©ІЦїв¶ҐІїГж»э![]() µДЧоґуФКРнЦµКЗ¶аЙЩЈї
µДЧоґуФКРнЦµКЗ¶аЙЩЈї
ЈЁ2Ј©ОЄК№![]() ґпµЅЧоґуЈ¬¶шКµјКН¶ЧКУЦІ»і¬№эФ¤ЛгЈ¬ДЗГґХэГжМъХ¤У¦ЙијЖОЄ¶аі¤Јї
ґпµЅЧоґуЈ¬¶шКµјКН¶ЧКУЦІ»і¬№эФ¤ЛгЈ¬ДЗГґХэГжМъХ¤У¦ЙијЖОЄ¶аі¤Јї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ЛДАвЧ¶![]() ЦРЈ¬µЧГж
ЦРЈ¬µЧГж![]() КЗБвРО,
КЗБвРО,![]() КЗ
КЗ![]() µДЦРµгЈ¬µг
µДЦРµгЈ¬µг![]() ФЪІаАв
ФЪІаАв![]() ЙПЈ®
ЙПЈ®
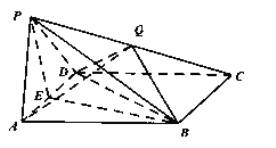
ЈЁ1Ј©ЗуЦ¤Јє![]() ЖЅГж
ЖЅГж![]() Ј»
Ј»
ЈЁ2Ј©Иф![]() КЗ
КЗ![]() µДЦРµгЈ¬ЗуЦ¤Јє
µДЦРµгЈ¬ЗуЦ¤Јє![]() ЖЅГж
ЖЅГж![]() Ј»
Ј»
ЈЁ3Ј©Иф![]() Ј¬КФЗу
Ј¬КФЗу![]() µДЦµЈ®
µДЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЅ«Хэ·ЅРО![]() СШ¶ФЅЗПЯ
СШ¶ФЅЗПЯ![]() ХЫіЙЦ±¶юГжЅЗ
ХЫіЙЦ±¶юГжЅЗ![]() Ј¬
Ј¬
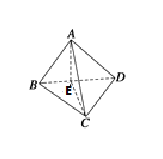
ўЩ![]() УлЖЅГж
УлЖЅГж![]() ЛщіЙЅЗµДґуРЎОЄ
ЛщіЙЅЗµДґуРЎОЄ![]()
ўЪ![]() КЗµИ±ЯИэЅЗРО
КЗµИ±ЯИэЅЗРО
ўЫ![]() Ул
Ул![]() ЛщіЙµДЅЗОЄ
ЛщіЙµДЅЗОЄ![]()
ўЬ![]()
ўЭ¶юГжЅЗ![]() ОЄ
ОЄ![]()
ФтЙПГжЅбВЫХэИ·µДОЄ_______Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЛщКѕµДјёєОМеЈ¬µЧГжABFEКЗ±Яі¤ОЄ2µДХэ·ЅРОЈ¬DEУлCFѕщґ№Ц±УЪЖЅГжABFEЈ¬ЗТ![]() Ј®
Ј®
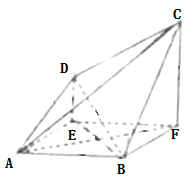
ЈЁ1Ј©Ц¤ГчЈєBEЎОЖЅГжACDЈ»
ЈЁ2Ј©ЗуИэАвЧ¶B©ЃACDµДМе»эЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіРЈПлБЛЅвёЯ¶юКэС§іЙјЁФЪС§ТµЛ®ЖЅїјКФЦРµДЗйїцЈ¬ґУЦРЛж»ъійіц![]() ИЛµДКэС§іЙјЁЧчОЄСщ±ѕІўЅшРРНіјЖЈ¬ЖµВК·ЦІј±нИзПВ±нЛщКѕ.
ИЛµДКэС§іЙјЁЧчОЄСщ±ѕІўЅшРРНіјЖЈ¬ЖµВК·ЦІј±нИзПВ±нЛщКѕ.
ЧйєЕ | ·ЦЧй | ЖµКэ | ЖµВК |
µЪ1Чй |
|
|
|
µЪ2Чй |
|
|
|
µЪ3Чй |
|
|
|
µЪ4Чй |
|
|
|
µЪ5Чй |
|
|
|
єПјЖ |
|
| |
ЈЁ1Ј©ѕЭґЛ№АјЖХвґОІОјУКэС§їјКФµДёЯ¶юС§ЙъµДКэС§ЖЅѕщіЙјЁЈ»
ЈЁ2Ј©ґУХвОеЧйЦРійИЎ![]() ИЛЅшРРЧщМёЈ¬ИфійИЎµДХв
ИЛЅшРРЧщМёЈ¬ИфійИЎµДХв![]() ИЛЦРЈ¬ЗЎєГУР
ИЛЦРЈ¬ЗЎєГУР![]() ИЛіЙјЁОЄ
ИЛіЙјЁОЄ![]() ·ЦЈ¬
·ЦЈ¬![]() ИЛіЙјЁОЄ
ИЛіЙјЁОЄ![]() ·ЦЈ¬
·ЦЈ¬![]() ИЛіЙјЁОЄ
ИЛіЙјЁОЄ![]() ·ЦЈ¬
·ЦЈ¬![]() ИЛіЙјЁОЄ
ИЛіЙјЁОЄ![]() ·ЦЈ¬ЗуХв
·ЦЈ¬ЗуХв![]() ИЛКэС§іЙјЁµД·ЅІоЈ»
ИЛКэС§іЙјЁµД·ЅІоЈ»
ЈЁ3Ј©ґУ![]() ИЛµДСщ±ѕЦРЈ¬Лж»ъійИЎІвКФіЙјЁФЪ
ИЛµДСщ±ѕЦРЈ¬Лж»ъійИЎІвКФіЙјЁФЪ![]() ДЪµДБЅГыС§ЙъЈ¬ЙиЖдІвКФіЙјЁ·Ц±рОЄ
ДЪµДБЅГыС§ЙъЈ¬ЙиЖдІвКФіЙјЁ·Ц±рОЄ![]() Ј¬
Ј¬![]() .
.
ЈЁiЈ©ЗуКВјюЎ°![]() Ў±µДёЕВКЈ»
Ў±µДёЕВКЈ»
ЈЁiiЈ©ЗуКВјюЎ°![]() Ў±µДёЕВК.
Ў±µДёЕВК.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИф¶ЇФІУлФІ![]() НвЗРЈ¬ЗТУлЦ±ПЯ
НвЗРЈ¬ЗТУлЦ±ПЯ![]() ПаЗРЈ¬Фт¶ЇФІФІРДµД№мјЈ·ЅіМКЗЈЁ Ј©
ПаЗРЈ¬Фт¶ЇФІФІРДµД№мјЈ·ЅіМКЗЈЁ Ј©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com