
【题目】某工厂有工人1000名,为了提高工人的生产技能,特组织工人参加培训.其中250名工人参加过短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人).现从该工厂的工人中共抽查了100名工人作为样本,调查他们的生产能力(生产能力是指工人一天加工的零件数),得到
类工人).现从该工厂的工人中共抽查了100名工人作为样本,调查他们的生产能力(生产能力是指工人一天加工的零件数),得到![]() 类工人生产能力的茎叶图(图1),
类工人生产能力的茎叶图(图1),![]() 类工人生产能力的频率分布直方图(图2).
类工人生产能力的频率分布直方图(图2).
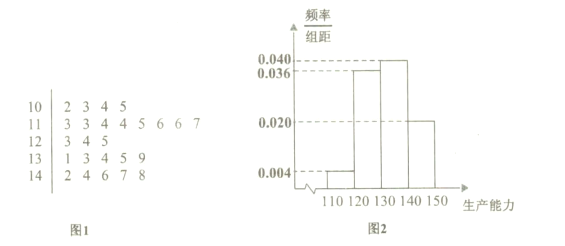
(1)在样本中求![]() 类工人生产能力的中位数,并估计
类工人生产能力的中位数,并估计![]() 类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(2)若规定生产能力在![]() 内为能力优秀,现以样本中频率作为概率,从1000名工人中按分层抽样共抽取
内为能力优秀,现以样本中频率作为概率,从1000名工人中按分层抽样共抽取![]() 名工人进行调查,请估计这
名工人进行调查,请估计这![]() 名工人中的各类人数,完成下面的
名工人中的各类人数,完成下面的![]() 列联表.
列联表.

若研究得到在犯错误的概率不超过![]() 的前提下,认为生产能力与培训时间长短有关,则
的前提下,认为生产能力与培训时间长短有关,则![]() 的最小值为多少?
的最小值为多少?
参考数据:

参考公式: 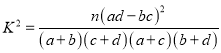 ,其中
,其中![]() .
.
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 分别是海岸线
分别是海岸线![]() 上的三个集镇,
上的三个集镇, ![]() 位于
位于![]() 的正南方向
的正南方向![]() 处,
处, ![]() 位于
位于![]() 的北偏东60°方向
的北偏东60°方向![]() 处;
处;
(1)为了缓解集镇![]() 的交通压力,拟在海岸线
的交通压力,拟在海岸线![]() 上分别修建码头
上分别修建码头![]() ,开辟水上直达航线,使
,开辟水上直达航线,使![]() ,
, ![]() .勘测时发现以
.勘测时发现以![]() 为圆心,
为圆心, ![]() 为半径的扇形区域为浅水区,不适宜船只航行,问此航线是否影响船只航行?
为半径的扇形区域为浅水区,不适宜船只航行,问此航线是否影响船只航行?
(2)为了发展经济需要,政府计划填海造陆,建造一个商业区(如图四边形![]() 所示),其中
所示),其中![]() ,
, ![]() ,
, ![]() ,求该商业区的面积
,求该商业区的面积![]() 的取值范围.
的取值范围.
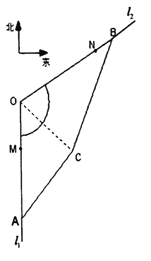
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)当![]() 时,函数
时,函数![]() 恒有意义,求实数
恒有意义,求实数![]() 的取值范围;
的取值范围;
(2)是否存在这样的实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上为减函数,并且最大值为1?如果存在,试求出
上为减函数,并且最大值为1?如果存在,试求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海关对同时从![]() 三个不同地区进口的某种商品进行随机抽样检测,已知从
三个不同地区进口的某种商品进行随机抽样检测,已知从![]() 三个地区抽取的商品件数分别是50,150,100.检测人员再用分层抽样的方法从海关抽样的这些商品中随机抽取6件样品进行检测.
三个地区抽取的商品件数分别是50,150,100.检测人员再用分层抽样的方法从海关抽样的这些商品中随机抽取6件样品进行检测.
(1)求这6件样品中,来自![]() 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往另一机构进行进一步检测,求这2件样品来自相同地区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com